题目内容
若x，y∈R，且x2+y2=1．当x+y+c=0时，c的最大值是（ ）A．
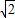
B．
C．
D．
【答案】分析：根据题意设y=cosα，x=sinα，由x+y+c=0，得到c=-x-y，将设出的x与y代入，利用两角和与差的正弦函数公式化为一个角的正弦函数，根据正弦函数的图象与性质即可求出c的最大值．
解答：解：根据题意设y=cosα，x=sinα，
将x+y+c=0变形为c=-x-y=-cosα-sinα=-
sin（α+
），
∴-
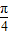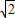≤c≤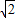
，
则c的最大值为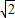
．
故选A
点评：此题考查了直线与圆相交的性质，涉及的知识有：两角和与差的正弦函数公式，以及正弦函数的定义域以及值域，将c变形为一个角的正弦函数是解本题的关键．
解答：解：根据题意设y=cosα，x=sinα，
将x+y+c=0变形为c=-x-y=-cosα-sinα=-
sin（α+），∴-
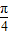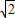≤c≤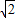，则c的最大值为
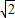．故选A
点评：此题考查了直线与圆相交的性质，涉及的知识有：两角和与差的正弦函数公式，以及正弦函数的定义域以及值域，将c变形为一个角的正弦函数是解本题的关键．
练习册系列答案
相关题目