题目内容
在区间[-2,2]上任取两实数a,b,则二次方程x2-ax+b2=0有实数解的概率为________.

分析:本题是一个等可能事件的概率,试验发生包含的事件是在区间[-2,2]上任取两个数a和b,写出事件对应的集合,做出面积,满足条件的事件是关于x的方程x2-ax+b2=0有实数根,根据二次方程的判别式写出a,b要满足的条件,写出对应的集合,做出面积,得到概率.
解答:
 解:由题意知本题是一个等可能事件的概率,
解:由题意知本题是一个等可能事件的概率,∵试验发生包含的事件是在区间[-2,2]上任取两个数a和b,
事件对应的集合是Ω={(a,b)|-2≤a≤2,-2≤b≤2}
对应的面积是sΩ=16,
满足条件的事件是关于x的方程x2-ax+b2=0有实数根,
即a2-4b2≥0,
∴
 或
或 ,
,事件对应的集合是A={(a,b)|0≤a≤1,0≤b≤1,|a|≥2|b|}
对应的图形的面积是sA=4S△OAB=4×
 1=4
1=4∴根据等可能事件的概率得到P=

故答案为:
 .
.点评:本题考查几何概型,古典概型和几何概型是我们学习的两大概型,古典概型要求能够列举出所有事件和发生事件的个数,而不能列举的就是几何概型,几何概型的概率的值是通过长度、面积、和体积、的比值得到.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
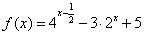 在区间[-2,2]上的最大值,并求函数f(x)取得最大值时的x的取值;
在区间[-2,2]上的最大值,并求函数f(x)取得最大值时的x的取值;  在区间[-2,2]上的最大值为14,求实数a的值。
在区间[-2,2]上的最大值为14,求实数a的值。