题目内容
已知双曲线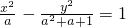 的离心率的范围是数集M,设p:“k∈M”; q:“函数f(x)=
的离心率的范围是数集M,设p:“k∈M”; q:“函数f(x)=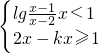 的值域为R”.则P是Q成立的
的值域为R”.则P是Q成立的
- A.充分而不必要条件
- B.必要而不充分条件
- C.充分必要条件
- D.既不充分也不必要条件
C
分析:先求出双曲线的离心率,利用基本不等式可求其范围,从而可得数集M;先求分段函数的值域,从而利用充要条件的判断方法,即可判断.
解答:双曲线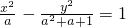 的离心率为
的离心率为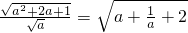
∵a>0
∴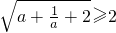
∴M=[2,+∞)
当x<1时,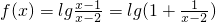 ,
,
∵x<1,∴x-2<-1,∴ ,
,
∴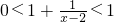 ,∴f(x)<0
,∴f(x)<0
当x≥1时,f(x)=2x-k≥2-k
∴若k≥2,则f(x)的值域为R;
若f(x)的值域为R,则2-k≤0,∴k≥2,
∴P是Q的充要条件
故选C.
点评:本题以充要条件为载体,考查双曲线的离心率,考查分段函数的值域,解题的关键是求出相应的范围.
分析:先求出双曲线的离心率,利用基本不等式可求其范围,从而可得数集M;先求分段函数的值域,从而利用充要条件的判断方法,即可判断.
解答:双曲线
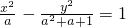 的离心率为
的离心率为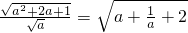
∵a>0
∴
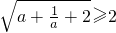
∴M=[2,+∞)
当x<1时,
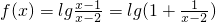 ,
,∵x<1,∴x-2<-1,∴
 ,
,∴
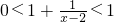 ,∴f(x)<0
,∴f(x)<0当x≥1时,f(x)=2x-k≥2-k
∴若k≥2,则f(x)的值域为R;
若f(x)的值域为R,则2-k≤0,∴k≥2,
∴P是Q的充要条件
故选C.
点评:本题以充要条件为载体,考查双曲线的离心率,考查分段函数的值域,解题的关键是求出相应的范围.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
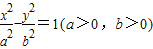 的左、右焦点分别为F1(-c,0),F2(c,0),若双曲线上存在一点P使
的左、右焦点分别为F1(-c,0),F2(c,0),若双曲线上存在一点P使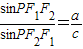 ,则该双曲线的离心率的取值范围是.
,则该双曲线的离心率的取值范围是.  的左、右焦点分别为F1(-c,0),F2(c,0),若双曲线上存在一点P使
的左、右焦点分别为F1(-c,0),F2(c,0),若双曲线上存在一点P使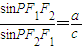 ,则该双曲线的离心率的取值范围是.
,则该双曲线的离心率的取值范围是. 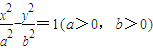 的左、右焦点分别为F1(-c,0),F2(c,0),若双曲线上存在一点P使
的左、右焦点分别为F1(-c,0),F2(c,0),若双曲线上存在一点P使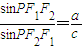 ,则该双曲线的离心率的取值范围是.
,则该双曲线的离心率的取值范围是. 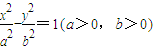 的左、右焦点分别为F1(-c,0),F2(c,0),若双曲线上存在一点P使
的左、右焦点分别为F1(-c,0),F2(c,0),若双曲线上存在一点P使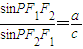 ,则该双曲线的离心率的取值范围是.
,则该双曲线的离心率的取值范围是. 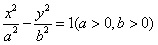 的左、右焦点分别为F1(-c,0),F2(c,0),若双曲线上存在一点P使
的左、右焦点分别为F1(-c,0),F2(c,0),若双曲线上存在一点P使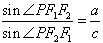 ,则该双曲线的离心率的取值范围是( )。
,则该双曲线的离心率的取值范围是( )。