题目内容
函数f(x)=logax(a>0且a≠1)对任意正实数x,y都有( )A.f=f(x)•f(y)
B.f=f(x)+f(y)
C.f(x+y)=f(x)•f(y)
D.f(x+y)=f(x)+f(y)
【答案】分析:利用对数的运算法则,得到对任意正实数x,y都有:f(x•y)=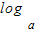 (x•y)=logax+logay=f(x)+f(y).
(x•y)=logax+logay=f(x)+f(y).
解答:解:∵f(x)=logax(a>0且a≠1),
∴对任意正实数x,y都有:
f(x•y)=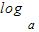 (x•y)=logax+logay=f(x)+f(y),
(x•y)=logax+logay=f(x)+f(y),
故选B.
点评:本题考查对数的运算性质,解题时要认真审题,仔细解答,注意合理地进行等价转化.
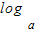 (x•y)=logax+logay=f(x)+f(y).
(x•y)=logax+logay=f(x)+f(y).解答:解:∵f(x)=logax(a>0且a≠1),
∴对任意正实数x,y都有:
f(x•y)=
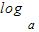 (x•y)=logax+logay=f(x)+f(y),
(x•y)=logax+logay=f(x)+f(y),故选B.
点评:本题考查对数的运算性质,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
已知函数f(x)=log -
(x2-ax+3a)在[2,+∞)上是减函数,则实数a的范围是( )
| 1 |
| 2 |
| A、(-∞,4] |
| B、(-4,4] |
| C、(0,12) |
| D、(0,4] |