题目内容
△ABC中,a、b、c分别是角A、B、C的对边,向量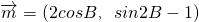 ,
, =(2sin2(
=(2sin2(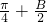 ),-1),
),-1), ⊥
⊥ .
.
(I)求角B的大小;
(II)若 ,求△ABC的周长的最大值.
,求△ABC的周长的最大值.
解:(I)∵ ,∴
,∴ ,∴
,∴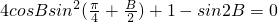 ,…(2分)
,…(2分)
∴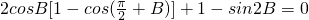 .
.
即2cosB+sin2B+1-sin2B=0,∴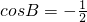 ,又B∈(0,π),∴
,又B∈(0,π),∴ . …(6分)
. …(6分)
(II)由正弦定理可得: ,又由(I)可知
,又由(I)可知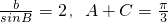 .
.
∴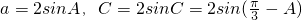 .…(8分)
.…(8分)
所以△ABC的周长为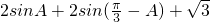 =
=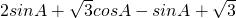 =
=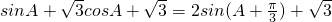 .…(10分)
.…(10分)
又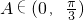 ,∴
,∴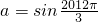 时,△ABC的周长有最大值为
时,△ABC的周长有最大值为 .…(12分)
.…(12分)
分析:(I) 由 可得
可得  ,解得
,解得 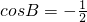 ,再由B∈(0,π)求得B的值.
,再由B∈(0,π)求得B的值.
(II)由正弦定理可得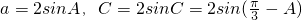 ,求得△ABC的周长为
,求得△ABC的周长为 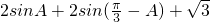 ,化简为
,化简为 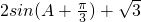 ,由此求得△ABC的周长有最大值
,由此求得△ABC的周长有最大值
点评:本题主要考查余弦定理的应用,两个向量垂直的性质,两角和的正弦公式,属于中档题.
 ,∴
,∴ ,∴
,∴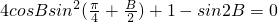 ,…(2分)
,…(2分)∴
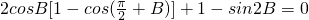 .
.即2cosB+sin2B+1-sin2B=0,∴
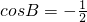 ,又B∈(0,π),∴
,又B∈(0,π),∴ . …(6分)
. …(6分)(II)由正弦定理可得:
 ,又由(I)可知
,又由(I)可知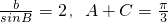 .
.∴
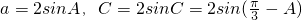 .…(8分)
.…(8分)所以△ABC的周长为
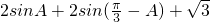 =
=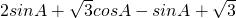 =
=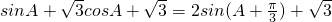 .…(10分)
.…(10分)又
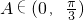 ,∴
,∴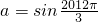 时,△ABC的周长有最大值为
时,△ABC的周长有最大值为 .…(12分)
.…(12分)分析:(I) 由
 可得
可得  ,解得
,解得 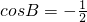 ,再由B∈(0,π)求得B的值.
,再由B∈(0,π)求得B的值.(II)由正弦定理可得
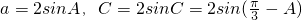 ,求得△ABC的周长为
,求得△ABC的周长为 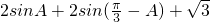 ,化简为
,化简为 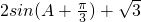 ,由此求得△ABC的周长有最大值
,由此求得△ABC的周长有最大值点评:本题主要考查余弦定理的应用,两个向量垂直的性质,两角和的正弦公式,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目