题目内容
(本题满分12分)如图,椭圆C方程为 (
( ),点
),点 为椭圆C的左、右顶点。
为椭圆C的左、右顶点。

(1)若椭圆C上的点到焦点的距离的最大值为3,最小值为1,求椭圆的标准方程;
(2)若直线 与(1)中所述椭圆C相交于A、B两点(A、B不是左、右顶点),且满足
与(1)中所述椭圆C相交于A、B两点(A、B不是左、右顶点),且满足 ,求证:直线
,求证:直线 过定点,并求出该点的坐标。
过定点,并求出该点的坐标。
【答案】
(1) 
(2) 
【解析】
试题分析:解:(1)
由题意知 
 椭圆的标准方程为
椭圆的标准方程为
(2)设 ,由
,由 …….(1)
…….(1)
联立方程
 带入(1)式整理的
带入(1)式整理的
所以得,
当 时,满足
时,满足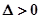 。此时,直线
。此时,直线 恒过点
恒过点
当 时,满足
时,满足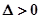 。此时,直线
。此时,直线 恒过点
恒过点 不符合题意,舍。
不符合题意,舍。
所以,直线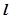 恒过定点
恒过定点 。
。
考点:椭圆的方程以及直线与椭圆的位置关系
点评:解决该试题的关键是利用椭圆性质来求解方程,同时能利用韦达定理和垂直关系得到结论,属于中档题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 为底面的直棱柱被平面
为底面的直棱柱被平面 所截而得.
所截而得.  ,
, 为
为 的中点.
的中点.
 时,求平面
时,求平面 为何值时,在棱
为何值时,在棱 上存在点
上存在点 ,使
,使 平面
平面 中,已知上下两底面为正方形,且边长均为1;侧棱
中,已知上下两底面为正方形,且边长均为1;侧棱 ,为
,为 中点,
中点, 为
为 中点,
中点, 为
为 上一个动点.
上一个动点.
 ;
; 的平
的平
 中,已知
中,已知 的直径
的直径 的中点.
的中点.
 所成角的正弦值.
所成角的正弦值.
