题目内容
已知函数 ,满足:①对任意
,满足:①对任意 ,都有
,都有
 ;
;
②对任意n∈N *都有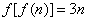 .
.
(Ⅰ)试证明: 为
为 上的单调增函数;
上的单调增函数;
(Ⅱ)求 ;
;
(Ⅲ)令 ,试证明:
,试证明:
【答案】
解:(I) 由①知,对任意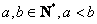 ,都有
,都有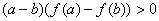 ,
,
由于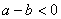 ,从而
,从而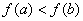 ,所以函数
,所以函数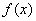 为
为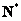 上的单调增函数
上的单调增函数
(II)令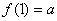 ,则
,则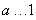 ,显然
,显然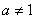 ,否则
,否则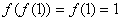 ,与
,与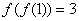 矛盾.从而
矛盾.从而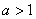 ,而由
,而由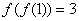 ,即得
,即得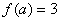 .
.
又由(I)知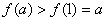 ,即
,即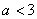 .
.
于是得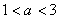 ,又
,又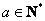 ,从而
,从而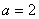 ,即
,即 .
.
进而由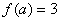 知,
知,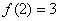 .
.
于是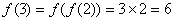 ,
,
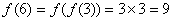 ,
,
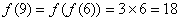 ,
,
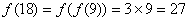 ,
,
 ,
,
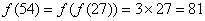 ,
由于
,
由于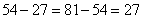 ,
,
而且由(I)知,函数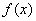 为单调增函数,因此
为单调增函数,因此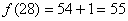 .
.
从而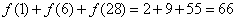 .
.
(Ⅲ)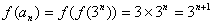 ,
,
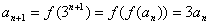 ,
,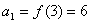 .
.
即数列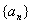 是以6为首项, 以3为公比的等比数列 .
是以6为首项, 以3为公比的等比数列 .
∴ 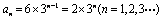
于是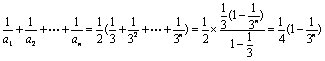 ,显然
,显然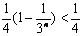 ,
,
另一方面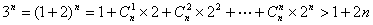 ,
,
从而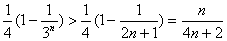 .
.
综上所述, 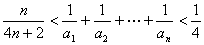 .
.

练习册系列答案
相关题目