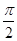题目内容
已知正方体的棱长为2,则它的内切球的表面积是 .
分析:根据正方体内切球和正方体的棱长关系,确定球的半径即可求出球的表面积.
解答:解:∵正方体的内切球的球心O到正方体各面的距离等于半径,
∴2R=2,
即球半径R=1,
∴内切球的表面积是4π.
故答案为:4π;
∴2R=2,
即球半径R=1,
∴内切球的表面积是4π.
故答案为:4π;
点评:本题主要考查球的表面积的计算,根据球与正方体的内切关系确定球的半径是解决本题的关键,比较基础.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
已知正方体的棱长为2,则其外接球的半径为( )
| A、2 | ||
B、2
| ||
C、2
| ||
D、
|
 的棱长为2,
的棱长为2, 分别是
分别是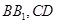 的中点.
的中点. 的体积;
的体积;
 的棱长为2, 长为2的线段
的棱长为2, 长为2的线段 的一个端点
的一个端点 在棱
在棱 上运动, 另一端点
上运动, 另一端点 在正方形
在正方形 内运动, 则
内运动, 则
 B.
B.
 D.
D.