题目内容
下列命题:(1)函数f(x)=cos4x-sin4x的最小正周期是π;
(2)已知向量
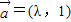 ,
,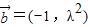 ,
,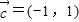 ,则
,则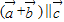 的充要条件是λ=-1;
的充要条件是λ=-1;(3)若
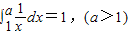 ,则a=e.
,则a=e.其中所有的真命题是( )
A.(3)
B.(1)(2)
C.(2)(3)
D.(1)(3)
【答案】分析:(1)利用半角公式对函数f(x)进行化简,再利用周期公式求出周期;
(2)根据向量平行的条件可得(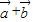 )=m
)=m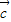 ,可以求出λ的值;
,可以求出λ的值;
(3)利用定积分公式,找出原函数谋求出a的值;
解答:解:(1)∵函数f(x)=cos4x-sin4=(cos2x-sin2x)(cos2x+sin2x)=(cos2x-sin2x)=cos2x,
∴T=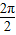 =π,f(x)的最小正周期是π,故(1)正确;
=π,f(x)的最小正周期是π,故(1)正确;
(2)∵已知向量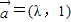 ,
,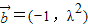 ,
,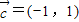 ,要使
,要使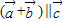 ,可得(
,可得(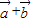 )=m
)=m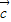 ,
,
∵(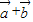 )=(λ-1,1+λ2),代入得
)=(λ-1,1+λ2),代入得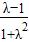 =-1,解得λ=0或-1,
=-1,解得λ=0或-1,
故(2)错误;
(3)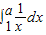 =
=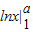 =lna-ln1=lna=1,可得a=e;
=lna-ln1=lna=1,可得a=e;
故(3)正确;
故选D;
点评:此题考查三角函数的化简,向量共线的条件以及定积分计算,考察的知识点比较多,但都比较基础!
(2)根据向量平行的条件可得(
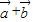 )=m
)=m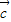 ,可以求出λ的值;
,可以求出λ的值;(3)利用定积分公式,找出原函数谋求出a的值;
解答:解:(1)∵函数f(x)=cos4x-sin4=(cos2x-sin2x)(cos2x+sin2x)=(cos2x-sin2x)=cos2x,
∴T=
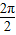 =π,f(x)的最小正周期是π,故(1)正确;
=π,f(x)的最小正周期是π,故(1)正确;(2)∵已知向量
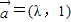 ,
,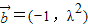 ,
,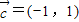 ,要使
,要使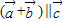 ,可得(
,可得(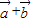 )=m
)=m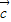 ,
,∵(
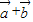 )=(λ-1,1+λ2),代入得
)=(λ-1,1+λ2),代入得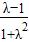 =-1,解得λ=0或-1,
=-1,解得λ=0或-1,故(2)错误;
(3)
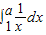 =
=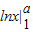 =lna-ln1=lna=1,可得a=e;
=lna-ln1=lna=1,可得a=e;故(3)正确;
故选D;
点评:此题考查三角函数的化简,向量共线的条件以及定积分计算,考察的知识点比较多,但都比较基础!

练习册系列答案
相关题目