Question

方程lgx+x-3=0的根所在的区间是

1. A.
   （1，2）
2. B.
   （2，3）
3. C.
   （3，4）
4. D.
   （0，1）

Answer 1

B
分析：在同一平面直角坐标系中，画出函数y=lgx与y=-x+3的图象．它们的交点横坐标x₀，显然在区间（1，3）内，由于画图精确性的限制，单凭直观就比较困难了．实际上这是要比较x₀与2的大小．当x=2时，lgx=lg2，3-x=1．由于lg2＜1，因此x₀＞2，从而得到答案．
解答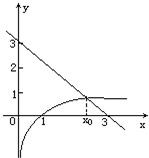：解：lgx+x-3=0可化为：lgx=-x+3，
在同一平面直角坐标系中，画出函数y=lgx与y=-x+3的图象．
它们的交点横坐标x₀．
当x=2时，lgx=lg2，3-x=1．
∵lg2＜1=lg10，
∴x₀＞2，
从而判定x₀∈（2，3）．
故选B．
点评：本题主要考查了函数的零点与方程根的关系，考查通过构造函数用数形结合法求方程lgx+x-3=0解所在的区间．数形结合，要在结合方面下功夫．不仅要通过图象直观估计，而且还要计算x₀的邻近两个函数值，通过比较其大小进行判断．