题目内容
设函数f(x)=
，则函数g（x）=f（x）-x的零点的个数为（ ）
|
| A、1 | B、2 | C、3 | D、4 |
分析：求函数g（x）=f（x）-x的零点个数，我们可以转化为求函数y=f（x）与函数y=x图象交点的个数，根据函数y=f（x）的解析式，我们在同一坐标系中分别画出两个函数图象由图象即可求出两个函数的交点个数，即函数g（x）=f（x）-x的零点个数．
解答：解：∵f(x)=
，则函数g（x）=f（x）-x的零点个数等价于
函数y=f（x）与函数y=x图象交点的个数，
∵当x＞0时，f（x）=f（x-1）
∴f（x）是周期函数，
当0＜x≤1，则x-1≤0，
∴f（x）=f（x-1）=（x-1）2，
在同一坐标系中画出两个函数图象如下图所示：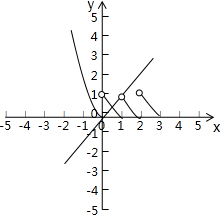
由图可知函数y=f（x）与函数y=x图象共有2个交点
故函数g（x）=f（x）-x的零点的个数有2个
故选：B
|
函数y=f（x）与函数y=x图象交点的个数，
∵当x＞0时，f（x）=f（x-1）
∴f（x）是周期函数，
当0＜x≤1，则x-1≤0，
∴f（x）=f（x-1）=（x-1）2，
在同一坐标系中画出两个函数图象如下图所示：
由图可知函数y=f（x）与函数y=x图象共有2个交点
故函数g（x）=f（x）-x的零点的个数有2个
故选：B
点评：本题考查的知识点是函数零点的判定定理，其中将求函数零点的问题转化为求两个函数图象交点的问题是解答本题的关键，体现了数形结合的数学思想方法，属中档题．
练习册系列答案
阅读快车系列答案
相关题目
设函数
设函数