题目内容
已知tana=4,tanβ=3,则tan(a+β)=
- A.-

- B.

- C.

- D.-
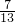
A
分析:先根据两角和的正切函数公式表示出tan(a+β)的关系式,然后把tana和tanβ的值代入关系式中即可求出tan(a+β)的值.
解答:因为tana=4,tanβ=3
则tan(a+β)= =
=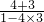 =-
=- ,
,
故选A
点评:此题考查学生灵活运用两角和的正切函数公式求值,是送分的题,做题时要细心.
分析:先根据两角和的正切函数公式表示出tan(a+β)的关系式,然后把tana和tanβ的值代入关系式中即可求出tan(a+β)的值.
解答:因为tana=4,tanβ=3
则tan(a+β)=
 =
=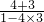 =-
=- ,
,故选A
点评:此题考查学生灵活运用两角和的正切函数公式求值,是送分的题,做题时要细心.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
已知tana=4,tanβ=3,则tan(a+β)=( )
A、-
| ||
B、
| ||
C、
| ||
D、-
|







