题目内容
已知离心率为 的椭圆
的椭圆 +
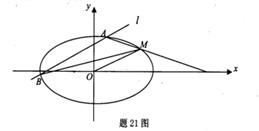
+ =1(a>b>0)与过点A(2,0)、B(0,1)的直线有且只有一个公共点P,点F是椭圆的右焦点.
=1(a>b>0)与过点A(2,0)、B(0,1)的直线有且只有一个公共点P,点F是椭圆的右焦点.
(Ⅰ)求椭圆的方程;
(Ⅱ)在x轴上是否存在一点M(m,0),使过M且与椭圆交于R、S两点的任意直线l,均满足∠RFP=∠SFP?若存在,求m的值;若不存在,请说明理由.
解:(Ⅰ)∵e=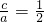 ,∴a=2c,b=
,∴a=2c,b=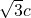 ,
,
设椭圆的方程为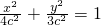 ,
,
直线AB的方程为y=-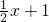 ,
,
由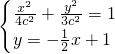 得x2-x+1-3c2=0,
得x2-x+1-3c2=0,
由题意知△=1-4(1-3c2)=0,
∴c= ,椭圆的方程为
,椭圆的方程为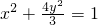 .
.
(Ⅱ)假设存在满足条件的点M,易知直线l的斜率不存在时,不合题意,
故设其斜率为k,则l的方程是y=k(x-m),
由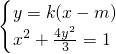 ,得(3+4k2)x2-8k2mx+4k2m2-3=0,
,得(3+4k2)x2-8k2mx+4k2m2-3=0,
设R(x1,y1),S(x2,y2),则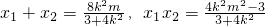 ,
,
∵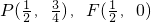 ,∴PF⊥x轴,
,∴PF⊥x轴,
∵∠RFP=∠SFP,∴kRF+kSP=0,
∴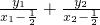 =
=
=
=0,
∴m=2.
∴m=2时,存在满足条件的点M(2,0).
分析:解(Ⅰ)由e=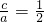 ,知a=2c,b=
,知a=2c,b=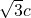 ,由此能求出椭圆的方程.
,由此能求出椭圆的方程.
(Ⅱ)设l的方程是y=k(x-m),由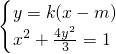 ,得(3+4k2)x2-8k2mx+4k2m2-3=0,设R(x1,y1),S(x2,y2),则
,得(3+4k2)x2-8k2mx+4k2m2-3=0,设R(x1,y1),S(x2,y2),则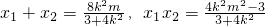 ,由PF⊥x轴,∠RFP=∠SFP,知kRF+kSP=0,由此能导出m=2时,存在满足条件的点M(2,0).
,由PF⊥x轴,∠RFP=∠SFP,知kRF+kSP=0,由此能导出m=2时,存在满足条件的点M(2,0).
点评:本题考查直线和圆锥曲线的位置关系,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.
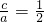 ,∴a=2c,b=
,∴a=2c,b=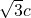 ,
,设椭圆的方程为
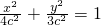 ,
,直线AB的方程为y=-
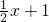 ,
,由
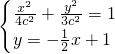 得x2-x+1-3c2=0,
得x2-x+1-3c2=0,由题意知△=1-4(1-3c2)=0,
∴c=
 ,椭圆的方程为
,椭圆的方程为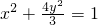 .
.(Ⅱ)假设存在满足条件的点M,易知直线l的斜率不存在时,不合题意,
故设其斜率为k,则l的方程是y=k(x-m),
由
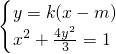 ,得(3+4k2)x2-8k2mx+4k2m2-3=0,
,得(3+4k2)x2-8k2mx+4k2m2-3=0,设R(x1,y1),S(x2,y2),则
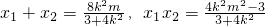 ,
,∵
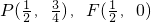 ,∴PF⊥x轴,
,∴PF⊥x轴,∵∠RFP=∠SFP,∴kRF+kSP=0,
∴
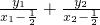 =
=
=

=0,
∴m=2.
∴m=2时,存在满足条件的点M(2,0).
分析:解(Ⅰ)由e=
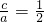 ,知a=2c,b=
,知a=2c,b=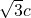 ,由此能求出椭圆的方程.
,由此能求出椭圆的方程.(Ⅱ)设l的方程是y=k(x-m),由
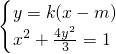 ,得(3+4k2)x2-8k2mx+4k2m2-3=0,设R(x1,y1),S(x2,y2),则
,得(3+4k2)x2-8k2mx+4k2m2-3=0,设R(x1,y1),S(x2,y2),则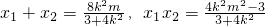 ,由PF⊥x轴,∠RFP=∠SFP,知kRF+kSP=0,由此能导出m=2时,存在满足条件的点M(2,0).
,由PF⊥x轴,∠RFP=∠SFP,知kRF+kSP=0,由此能导出m=2时,存在满足条件的点M(2,0).点评:本题考查直线和圆锥曲线的位置关系,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 的椭圆C1的顶点A1,A2恰好是双曲线
的椭圆C1的顶点A1,A2恰好是双曲线 的左右焦点,点P是椭圆上不同于A1,A2的任意一点,设直线PA1,PA2的斜率分别为k1,k2.
的左右焦点,点P是椭圆上不同于A1,A2的任意一点,设直线PA1,PA2的斜率分别为k1,k2. 时,圆C2:x2+y2-2mx=0被直线PA2截得弦长为
时,圆C2:x2+y2-2mx=0被直线PA2截得弦长为 ,求实数m的值.
,求实数m的值.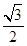 的椭圆
的椭圆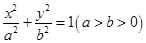 上的点到左焦点
上的点到左焦点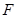 的最长距离为
的最长距离为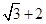 .
.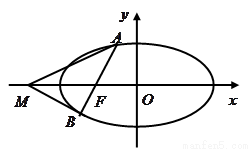
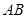 ,若点
,若点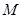 在
在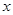 轴上,且使得
轴上,且使得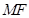 为
为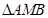 的一条内角平分线,则称点
的一条内角平分线,则称点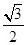 的椭圆
的椭圆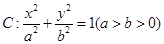 过点
过点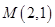 ,
,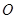 为坐标原点,平行于
为坐标原点,平行于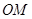 的直线
的直线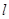 交椭圆于
交椭圆于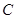 不同的两点
不同的两点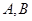 。
。
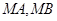 的斜率分别为
的斜率分别为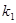 、
、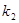 ,求证:
,求证: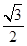 的椭圆
的椭圆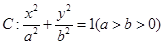 过点M(2,1),O为坐标原点,平行于OM的直线
过点M(2,1),O为坐标原点,平行于OM的直线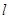 交椭圆C于不同的两点A、B。
交椭圆C于不同的两点A、B。 面积的最大值;
面积的最大值;