题目内容
坐标系与参数方程在极坐标系中,O为极点,半径为2的圆C的圆心的极坐标为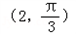 .
.
(1)求圆C的极坐标方程;
(2)P是圆C上一动点,点Q满足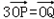 ,以极点O为原点,以极轴为x轴正半轴建立直角坐标系,求点Q的轨迹的直角坐标方程.
,以极点O为原点,以极轴为x轴正半轴建立直角坐标系,求点Q的轨迹的直角坐标方程.
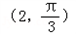 .
.(1)求圆C的极坐标方程;
(2)P是圆C上一动点,点Q满足
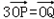 ,以极点O为原点,以极轴为x轴正半轴建立直角坐标系,求点Q的轨迹的直角坐标方程.
,以极点O为原点,以极轴为x轴正半轴建立直角坐标系,求点Q的轨迹的直角坐标方程.解:(1)(1)设M(ρ,θ)是圆C上任一点,
过C作CH⊥OM于H点,
则在RT△COH中,OH=OCsin∠COH,
而∠COH=∠COM=|θ﹣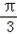 |,
|,
OH= OM=  ρ,OC=2,
ρ,OC=2,
所以 ρ=2cos|θ﹣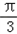 |,
|,
即ρ=4cos(θ﹣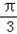 )为圆C的极坐标方程.
)为圆C的极坐标方程.
(2)设Q的极坐标为(ρ,θ),
由于 ,所以点P的极坐标为(
,所以点P的极坐标为( ρ,θ),
ρ,θ),
代入(1)中方程得  ρ=4cos(θ﹣
ρ=4cos(θ﹣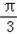 )
)
即ρ=6cosθ+6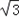 sinθ,
sinθ,
∴ρ2=6ρcosθ+6  ρsinθ,
ρsinθ,
所以点Q的轨迹的直角坐标方程为x2+y2﹣6x﹣6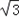 y=0
y=0

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
 (2012•江苏一模)选做题
(2012•江苏一模)选做题 选修4-4:坐标系与参数方程
选修4-4:坐标系与参数方程