题目内容
(2009江西卷理)(本小题满分14分)
各项均为正数的数列![]() ,
,![]() ,且对满足
,且对满足![]() 的正整数
的正整数![]() 都有
都有![]()
(1)当![]() 时,求通项
时,求通项![]()
![]()
![]()
(2)证明:对任意![]() ,存在与
,存在与![]() 有关的常数
有关的常数![]() ,使得对于每个正整数
,使得对于每个正整数![]() ,都有
,都有![]()
解析:(1)由![]() 得
得
![]() 将
将![]() 代入化简得
代入化简得 ![]()
![]()
![]()
所以![]()
![]()
![]()
故数列![]() 为等比数列,从而
为等比数列,从而
![]() 即
即![]()
可验证,![]() 满足题设条件.
满足题设条件.
(2) 由题设![]() 的值仅与
的值仅与![]() 有关,记为
有关,记为![]() 则
则![]()
![]()
![]()
考察函数 ![]() ,则在定义域上有
,则在定义域上有 ![]()
![]()
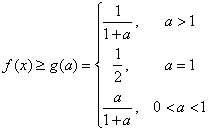
故对![]() ,
, ![]() 恒成立.
恒成立. ![]()
![]()
又 ![]() ,
,
注意到![]() ,解上式得
,解上式得
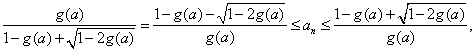
取![]() ,即有
,即有 ![]() .
. ![]()
![]()

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目