题目内容
已知圆C的方程为x2+y2+2x-7=0,圆心C关于原点对称的点为A,P是圆上任一点,线段AP的垂直平分线l交PC于点Q.(1)当点P在圆上运动时,求点Q的轨迹L的方程;
(2)过点B(1,
 )能否作出直线l2,使l2与轨迹L交于M、N两点,且点B是线段MN的中点,若这样的直线l2存在,请求出它的方程和M、N两点的坐标;若不存在,请说明理由.
)能否作出直线l2,使l2与轨迹L交于M、N两点,且点B是线段MN的中点,若这样的直线l2存在,请求出它的方程和M、N两点的坐标;若不存在,请说明理由.
【答案】分析:(1)由点Q是线段AP的垂直平分线l与CP的交点,可得|QP|=QA|.又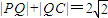 ,可得
,可得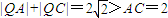 .利用椭圆的定义可知点Q的轨迹L为椭圆;
.利用椭圆的定义可知点Q的轨迹L为椭圆;
(2)假设直线l2存在,设M(x1,y1),N(x2,y2),分别代入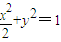 ,利用“点差法”、中点坐标公式及斜率公式即可得出直线l2的方程;与椭圆方程联立即可解得交点坐标.
,利用“点差法”、中点坐标公式及斜率公式即可得出直线l2的方程;与椭圆方程联立即可解得交点坐标.
解答:解:(1)如图,由已知圆C的方程x2+y2+2x-7=0,化为(x+1)2+y2=8,可得圆心C(-1,0),半径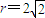 ,点A(1,0).
,点A(1,0).
∵点Q是线段AP的垂直平分线l与CP的交点,∴|QP|=QA|.
又∵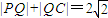 ,∴
,∴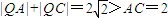 .
.
∴点Q的轨迹是以O为中心,C,A为焦点的椭圆,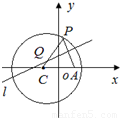
∵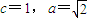 ,∴
,∴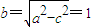 ,
,
∴点Q的轨迹L的方程为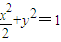 .
.
(2)假设直线l2存在,设M(x1,y1),N(x2,y2),分别代入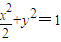 得
得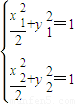 ,
,
两式相减得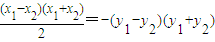 ,即
,即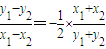 .
.
由题意,得x1+x2=2,y1+y2=1,
∴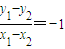 ,即kMN=-1.
,即kMN=-1.
∴直线l2的方程为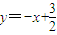 .
.
由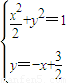 得6x2-12x+5=0.
得6x2-12x+5=0.
∵点B在椭圆L内,
∴直线l2的方程为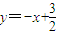 ,它与轨迹L存在两个交点,
,它与轨迹L存在两个交点,
解方程6x2-12x+5=0得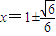 .
.
当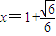 时,
时, ;当
;当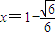 时,
时,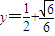 .
.
所以,两交点坐标分别为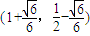 和
和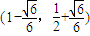 .
.
点评:本题综合考查了椭圆的定义、标准方程及其性质、“点差法”、中点坐标公式、直线与椭圆相交问题转化为方程联立得到一元二次方程等基础知识,考查了推理能力、数形结合的思想方法、计算能力、分析问题和解决问题的能力.
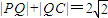 ,可得
,可得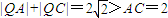 .利用椭圆的定义可知点Q的轨迹L为椭圆;
.利用椭圆的定义可知点Q的轨迹L为椭圆;(2)假设直线l2存在,设M(x1,y1),N(x2,y2),分别代入
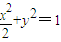 ,利用“点差法”、中点坐标公式及斜率公式即可得出直线l2的方程;与椭圆方程联立即可解得交点坐标.
,利用“点差法”、中点坐标公式及斜率公式即可得出直线l2的方程;与椭圆方程联立即可解得交点坐标.解答:解:(1)如图,由已知圆C的方程x2+y2+2x-7=0,化为(x+1)2+y2=8,可得圆心C(-1,0),半径
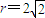 ,点A(1,0).
,点A(1,0).∵点Q是线段AP的垂直平分线l与CP的交点,∴|QP|=QA|.
又∵
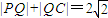 ,∴
,∴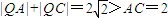 .
.∴点Q的轨迹是以O为中心,C,A为焦点的椭圆,

∵
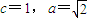 ,∴
,∴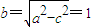 ,
,∴点Q的轨迹L的方程为
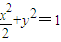 .
.(2)假设直线l2存在,设M(x1,y1),N(x2,y2),分别代入
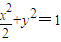 得
得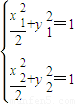 ,
,两式相减得
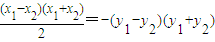 ,即
,即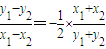 .
.由题意,得x1+x2=2,y1+y2=1,
∴
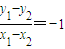 ,即kMN=-1.
,即kMN=-1.∴直线l2的方程为
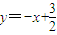 .
.由
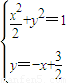 得6x2-12x+5=0.
得6x2-12x+5=0.∵点B在椭圆L内,
∴直线l2的方程为
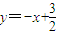 ,它与轨迹L存在两个交点,
,它与轨迹L存在两个交点,解方程6x2-12x+5=0得
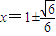 .
.当
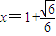 时,
时, ;当
;当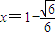 时,
时,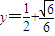 .
.所以,两交点坐标分别为
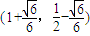 和
和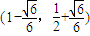 .
.点评:本题综合考查了椭圆的定义、标准方程及其性质、“点差法”、中点坐标公式、直线与椭圆相交问题转化为方程联立得到一元二次方程等基础知识,考查了推理能力、数形结合的思想方法、计算能力、分析问题和解决问题的能力.

练习册系列答案
相关题目