题目内容
已知双曲线 -y2=1的虚轴的上端点为B,过点B引直线l与双曲线的左支有两个不同的公共点,则直线l的斜率的取值范围是 .
-y2=1的虚轴的上端点为B,过点B引直线l与双曲线的左支有两个不同的公共点,则直线l的斜率的取值范围是 .
【答案】分析:双曲线 -y2=1的虚轴的上端点为B(0,1),由过点B引直线l与双曲线的左支有两个不同的公共点,知直线l的斜率k一定存在,且k>0,设直线l的方程为:y=kx+1,由
-y2=1的虚轴的上端点为B(0,1),由过点B引直线l与双曲线的左支有两个不同的公共点,知直线l的斜率k一定存在,且k>0,设直线l的方程为:y=kx+1,由 ,得
,得 ,设直线l与双曲线的左支交于A(x1,y1),B(x2,y2),由△>0,x1+x2<0,x1•x2>0,能求出直线l的斜率的取值范围.
,设直线l与双曲线的左支交于A(x1,y1),B(x2,y2),由△>0,x1+x2<0,x1•x2>0,能求出直线l的斜率的取值范围.
解答:解:双曲线 -y2=1的虚轴的上端点为B(0,1),
-y2=1的虚轴的上端点为B(0,1),
∵过点B引直线l与双曲线的左支有两个不同的公共点,
∴直线l的斜率k一定存在,且k>0,
设直线l的方程为:y=kx+1,
由 ,得
,得 ,
,
设直线l与双曲线的左支交于A(x1,y1),B(x2,y2),
则有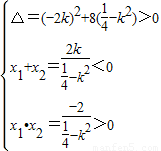 ,
,
解得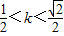 .
.
故答案为:( ).
).
点评:本题考查直线和双曲线的关系的综合应用,解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化.
 -y2=1的虚轴的上端点为B(0,1),由过点B引直线l与双曲线的左支有两个不同的公共点,知直线l的斜率k一定存在,且k>0,设直线l的方程为:y=kx+1,由
-y2=1的虚轴的上端点为B(0,1),由过点B引直线l与双曲线的左支有两个不同的公共点,知直线l的斜率k一定存在,且k>0,设直线l的方程为:y=kx+1,由 ,得
,得 ,设直线l与双曲线的左支交于A(x1,y1),B(x2,y2),由△>0,x1+x2<0,x1•x2>0,能求出直线l的斜率的取值范围.
,设直线l与双曲线的左支交于A(x1,y1),B(x2,y2),由△>0,x1+x2<0,x1•x2>0,能求出直线l的斜率的取值范围.解答:解:双曲线
 -y2=1的虚轴的上端点为B(0,1),
-y2=1的虚轴的上端点为B(0,1),∵过点B引直线l与双曲线的左支有两个不同的公共点,
∴直线l的斜率k一定存在,且k>0,
设直线l的方程为:y=kx+1,
由
 ,得
,得 ,
,设直线l与双曲线的左支交于A(x1,y1),B(x2,y2),
则有
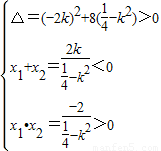 ,
,解得
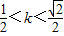 .
.故答案为:(
 ).
).点评:本题考查直线和双曲线的关系的综合应用,解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目