题目内容
设命题P:对任意实数,不等式x2-2x>m恒成立;命题:方程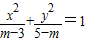 表示焦点在x轴上的双曲线.
表示焦点在x轴上的双曲线.(Ⅰ)若命题q为真命题,求实数m的取值范围;
(Ⅱ)若命题“p∨q””为真命题,且“p∧q”为假命题,求实数m的取值范围.
【答案】分析:(1)命题q为真命题,得方程 表示焦点在x轴上的双曲线,说明x2的分母为正数且y2的分母为负数.联列不等式组,解之即得实数m的取值范围;
表示焦点在x轴上的双曲线,说明x2的分母为正数且y2的分母为负数.联列不等式组,解之即得实数m的取值范围;
(2)先找出命题p真时,实数m的取值范围,再由“p∨q为真命题,p∧q为假命题”,说明“p真q假”成立,或“p假q真”成立,分这两种情况讨论,最后综合可得实数的取值范围.
解答:解:(1)若方程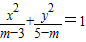 表示焦点在x轴上的双曲线,
表示焦点在x轴上的双曲线,
则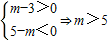
即命题q为真命题时,实数m的取值范围是(5,+∞)(5分)
(2)若命题p真,即对任意实数,不等式x2-2x-m>0恒成立.
∴△=4+4m<0,可得m<-1
p∨q为真命题,p∧q为假命题,说明“p真q假”成立,或“p假q真”成立,
①如果“p真q假”成立,则有 (9分)
(9分)
②如果“p假q真”成立,则有 (12分)
(12分)
所以实数的取值范围为m<-1或m>5(13分)
点评:本题以命题真假的判断为载体,着重考查了双曲线的标准方程和一元二次不等式的解集等知识点,属于基础题.
 表示焦点在x轴上的双曲线,说明x2的分母为正数且y2的分母为负数.联列不等式组,解之即得实数m的取值范围;
表示焦点在x轴上的双曲线,说明x2的分母为正数且y2的分母为负数.联列不等式组,解之即得实数m的取值范围;(2)先找出命题p真时,实数m的取值范围,再由“p∨q为真命题,p∧q为假命题”,说明“p真q假”成立,或“p假q真”成立,分这两种情况讨论,最后综合可得实数的取值范围.
解答:解:(1)若方程
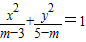 表示焦点在x轴上的双曲线,
表示焦点在x轴上的双曲线,则
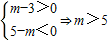
即命题q为真命题时,实数m的取值范围是(5,+∞)(5分)
(2)若命题p真,即对任意实数,不等式x2-2x-m>0恒成立.
∴△=4+4m<0,可得m<-1
p∨q为真命题,p∧q为假命题,说明“p真q假”成立,或“p假q真”成立,
①如果“p真q假”成立,则有
 (9分)
(9分)②如果“p假q真”成立,则有
 (12分)
(12分)所以实数的取值范围为m<-1或m>5(13分)
点评:本题以命题真假的判断为载体,着重考查了双曲线的标准方程和一元二次不等式的解集等知识点,属于基础题.

练习册系列答案
相关题目
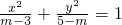 表示焦点在x轴上的双曲线.
表示焦点在x轴上的双曲线.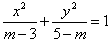 表示焦点在x轴上的双曲线,
表示焦点在x轴上的双曲线,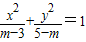 表示焦点在x轴上的双曲线.
表示焦点在x轴上的双曲线.