题目内容
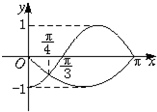已知函数y=f（x）是偶函数，y=g（x）是奇函数，它们的定义域为[-π，π]，且它们在x∈[0，π]上的图象如图所示，则不等式| f(x) |
| g(x) |
分析：由不等式
＞0 可知f（x），g（x）的函数值同号，观察图象选择函数值同号的部分，再由f（x）是偶函数，g（x）是奇函数，得到f（x）g（x）是奇函数，从而求得对称区间上的部分，最后两部分取并集．
| f(x) |
| g(x) |
解答：解：x∈[0，π]，由不等式
＞0 可知f（x），g（x）的函数值同号，即f（x）g（x）＞0
根据图象可知，当x＞0时，其解集为：(0，
)
∵y=f（x）是偶函数，y=g（x）是奇函数
∴f（x）g（x）是奇函数
∴当x＜0时，f（x）g（x）＜0，∴其解集为：(-
，-π)
综上：不等式
＞0 的解集是 (-π， -
)∪(0，
)
故选B．
| f(x) |
| g(x) |
根据图象可知，当x＞0时，其解集为：(0，
| π |
| 3 |
∵y=f（x）是偶函数，y=g（x）是奇函数
∴f（x）g（x）是奇函数
∴当x＜0时，f（x）g（x）＜0，∴其解集为：(-
| π |
| 3 |
综上：不等式
| f(x) |
| g(x) |
| π |
| 3 |
| π |
| 3 |
故选B．
点评：本题以函数的图象为载体，考查函数的奇偶性在解不等式中的应用，考查数形结合，转化，分类讨论等思想方法，解题的关键是不等式
＞0 可知f（x），g（x）的函数值同号，即f（x）g（x）＞0．
| f(x) |
| g(x) |
练习册系列答案
相关题目
已知函数y=f（x）是定义在R上的奇函数，当x＞0 时，f（x）的图象如图所示，则不等式x[f（x）-f（-x）]≤0 的解集为
已知函数y=f（x）的图象如图，则满足