题目内容
一位游客欲参观上海世博会中甲、乙、丙这3个展览馆,又该游客参观甲、乙、丙这3个展览馆的概率分别是0.4,0.5,0.6,且是否参观哪个展览馆互不影响.设ξ表示该游客离开上海世博会时参观的展览馆数与没有参观的展览馆数之差的绝对值.(Ⅰ)求ξ的概率分布及数学期望;
(Ⅱ)记“函数f(x)=x2-3ξx+1在区间[2,+∞)上单调递增”为事件A,求事件A的概率.
【答案】分析:(Ⅰ)欲求ξ的概率分布,由于ξ的可能取值为1,3.故只要利用相互独立事件的概率公式,分别求出这两个值的概率即可;最后再利用数学期望的计算公式求解即可.
(Ⅱ)先计算出事件A对应的ξ的值,再利用(I)中分布表求出其概率即可.
解答:解:(Ⅰ)分别记“客人参观甲展览馆”,“客人参观乙展览馆”,
“客人参观丙展览馆”为事件A1,A2,A3.由已知A1,A2,A3相互独立,
P(A1)=0.4,P(A2)=0.5,P(A3)=0.6.
客人参观的展览馆数的可能取值为0,1,2,3.
相应地,客人没有参观的展览馆数的可能取值为3,2,1,0,所以ξ的可能取值为1,3.
P(ξ=3)=P(A1•A2•A3)+P(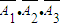 )=P(A1)P(A2)P(A3)+P(
)=P(A1)P(A2)P(A3)+P(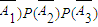 )
)
=2×0.4×0.5×0.6=0.24,P(ξ=1)=1-0.24=0.76,所以ξ的概率分布表为
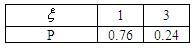 (5分)
(5分)
∴Eξ=1×0.76+3×0.24=1.48(6分)
(Ⅱ)因为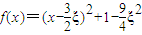 ,
,
所以函数f(x)=x2-3ξx+1在区间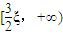 上单调递增,
上单调递增,
要使f(x)在[2,+∞)上单调递增,当且仅当
从而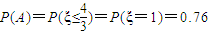 (10分)
(10分)
点评:本题主要考查了相互独立事件的概率乘法公式、离散型随机变量及其分布列及离散型随机变量的期望与方差,属于基础题.
(Ⅱ)先计算出事件A对应的ξ的值,再利用(I)中分布表求出其概率即可.
解答:解:(Ⅰ)分别记“客人参观甲展览馆”,“客人参观乙展览馆”,
“客人参观丙展览馆”为事件A1,A2,A3.由已知A1,A2,A3相互独立,
P(A1)=0.4,P(A2)=0.5,P(A3)=0.6.
客人参观的展览馆数的可能取值为0,1,2,3.
相应地,客人没有参观的展览馆数的可能取值为3,2,1,0,所以ξ的可能取值为1,3.
P(ξ=3)=P(A1•A2•A3)+P(
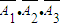 )=P(A1)P(A2)P(A3)+P(
)=P(A1)P(A2)P(A3)+P(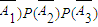 )
)=2×0.4×0.5×0.6=0.24,P(ξ=1)=1-0.24=0.76,所以ξ的概率分布表为
 (5分)
(5分)∴Eξ=1×0.76+3×0.24=1.48(6分)
(Ⅱ)因为
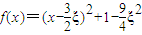 ,
,所以函数f(x)=x2-3ξx+1在区间
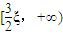 上单调递增,
上单调递增,要使f(x)在[2,+∞)上单调递增,当且仅当

从而
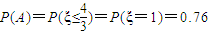 (10分)
(10分)点评:本题主要考查了相互独立事件的概率乘法公式、离散型随机变量及其分布列及离散型随机变量的期望与方差,属于基础题.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
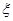 表示该游客离开上海世博会时参观的展览馆数与没有参观的展览馆数之差的绝对值.
表示该游客离开上海世博会时参观的展览馆数与没有参观的展览馆数之差的绝对值.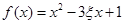 在区间
在区间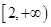 上单调递增”为事件
上单调递增”为事件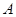 ,求事件
,求事件