题目内容
在△ABC中,顶点A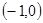 ,B
,B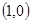 ,动点D,E满足:①
,动点D,E满足:① ;②
;②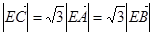 ,③
,③ 共线.
共线.
(Ⅰ)求△ABC顶点C的轨迹方程;
(Ⅱ)是否存在圆心在原点的圆,只要该圆的切线与顶点C的轨迹有两个不同交点M,N,就一定有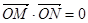 ,若存在,求该圆的方程;若不存在,请说明理由.
,若存在,求该圆的方程;若不存在,请说明理由.
【答案】
(I)设C(x,y),由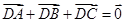 得,动点
得,动点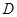 的坐标为
的坐标为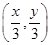 ;
;
由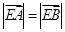 得,动点E在y轴上,再结合
得,动点E在y轴上,再结合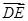 与
与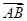 共线,
共线,
得,动点E的坐标为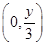 ;
…………2分
;
…………2分
由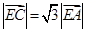 的,
的, ,
,
整理得,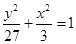 .
.
因为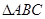 的三个顶点不共线,所以
的三个顶点不共线,所以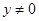 ,
,
故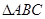 顶点C的轨迹方程为
顶点C的轨迹方程为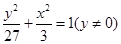 .…………5分
.…………5分
(II)假设存在这样的圆,其方程为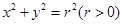 ,
,
当直线MN的斜率存在时,设其方程为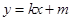 ,代入椭圆的方程,
,代入椭圆的方程,
得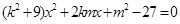 ,
,
设M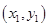 ,N
,N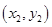 ,
,
则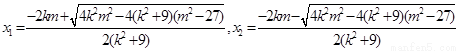 ,
,
所以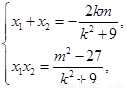 (*)…………7分
(*)…………7分
由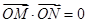 ,得
,得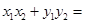 0,
0,
即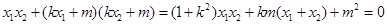 ,
,
将式子(*)代入上式,得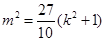 .…………9分
.…………9分
又直线MN: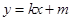 与圆
与圆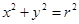 相切知:
相切知: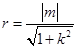 .
.
所以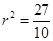 ,即存在圆
,即存在圆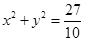 满足题意;
满足题意;
当直线MN的斜率不存在时,可得 ,
,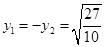 满足
满足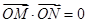 .
.
综上所述:存在圆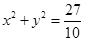 满足题意.
满足题意.
【解析】略

练习册系列答案
相关题目
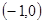 ,B
,B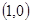 ,动点D,E满足:①
,动点D,E满足:①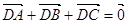 ;②
;②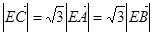 ,③
,③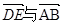 共线.
共线. 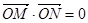 ,若存在,求该圆的方程;若不存在,请说明理由.
,若存在,求该圆的方程;若不存在,请说明理由.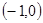 ,B
,B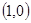 ,动点D,E满足:①
,动点D,E满足:①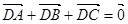 ;②
;②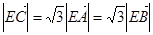 ,③
,③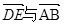 共线.
共线. 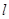 与动点C的轨迹交与M,N两点,且
与动点C的轨迹交与M,N两点,且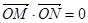 ,求直线
,求直线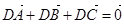 ;②|
;②|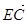 |=
|=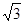 |
|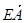 |=
|=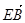 |③
|③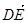 与
与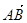 共线.
共线.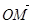 ·
·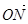 =0,求直线l的方程.
=0,求直线l的方程.