题目内容
已知函数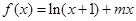 ,当
,当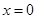 时,函数
时,函数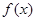 取得极大值.
取得极大值.
(1)求实数 的值;
的值;
(2)已知结论:若函数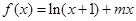 在区间
在区间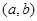 内导数都存在,且
内导数都存在,且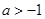 ,则存在
,则存在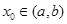 ,使得
,使得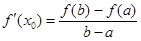 .试用这个结论证明:若
.试用这个结论证明:若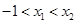 ,函数
,函数 ,则对任意
,则对任意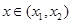 ,都有
,都有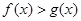 ;
;
(3)已知正数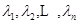 ,满足
,满足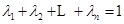 ,求证:当
,求证:当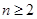 ,
,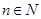 时,对任意大于
时,对任意大于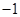 ,且互不相等的实数
,且互不相等的实数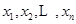 ,都有
,都有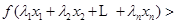
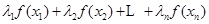 .
.
【答案】
(1)-1;(2)(3)见解析.
【解析】本试题主要是考查了导数在研究函数中的运用。并和不等式进行综合的试题。有难度。
解:(1)
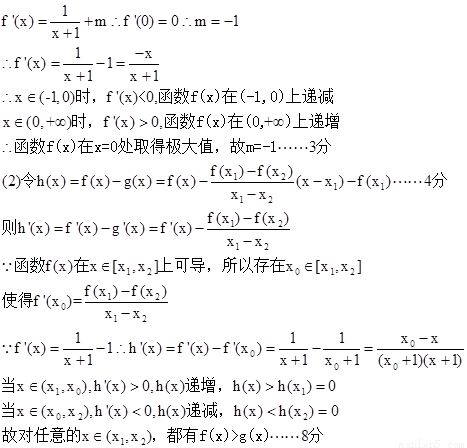
(3)用数学归纳法证明.
①当n=2时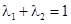 ,,且
,,且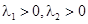 ,,
,,
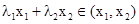 ,
,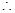 由(Ⅱ)得
由(Ⅱ)得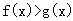 ,即
,即
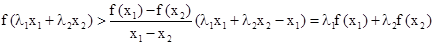 ,
,
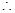 当n=2时,结论成立. …………………………9分
当n=2时,结论成立. …………………………9分
②假设当n=k时结论成立,即当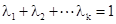 时,
时,
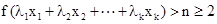 . 当n=k+1时,设正数
. 当n=k+1时,设正数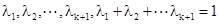 ,令
,令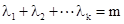 ,
,
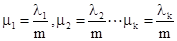 , 则
, 则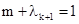 ,且
,且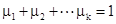 .
.
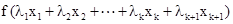
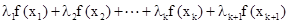 …………………………13分
…………………………13分
 当n=k+1时,结论也成立.
当n=k+1时,结论也成立.
综上由①②,对任意 ,结论恒成立. …………………………14分
,结论恒成立. …………………………14分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
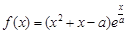 (
(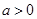 ).
).
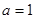 时,求函数
时,求函数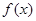 的单调区间;
的单调区间;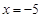 时,
时,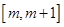
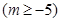 上的最小值;
上的最小值; 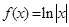
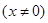 ,函数
,函数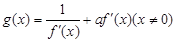
 时,求函数
时,求函数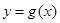 的表达式;
的表达式;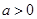 ,函数
,函数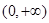 上的最小值是2 ,求
上的最小值是2 ,求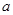 的值;
的值;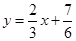 与函数
与函数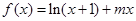 ,当
,当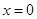 时,函数
时,函数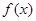 取得极大值.
取得极大值.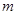 的值;(Ⅱ)已知结论:若函数
的值;(Ⅱ)已知结论:若函数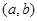 内导数都存在,且
内导数都存在,且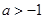 ,则存在
,则存在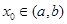 ,使得
,使得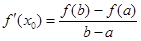 .试用这个结论证明:若
.试用这个结论证明:若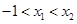 ,函数
,函数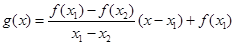 ,则对任意
,则对任意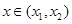 ,都有
,都有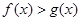 ;(Ⅲ)已知正数
;(Ⅲ)已知正数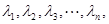 满足
满足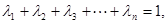 求证:当
求证:当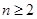 ,
,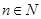 时,对任意大于
时,对任意大于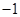 ,且互不相等的实数
,且互不相等的实数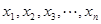 ,都有
,都有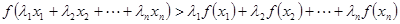
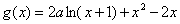
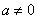 时,讨论函数
时,讨论函数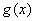 的单调性:
的单调性: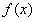 的图像上存在不同两点
的图像上存在不同两点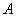 ,
,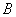 ,设线段
,设线段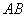 的中点为
的中点为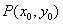 ,使得
,使得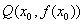 处的切线
处的切线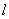 与直线
与直线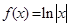
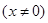 ,函数
,函数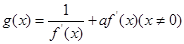
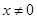 时,求函数
时,求函数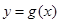 的表达式;
的表达式;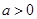 ,函数
,函数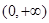 上的最小值是2 ,求
上的最小值是2 ,求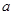 的值;
的值;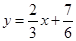
 与函数
与函数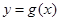 的图象所围成图形的面积.
的图象所围成图形的面积.