题目内容
设A，B是两个定点，且|AB|=2，动点M到A点的距离是4，线段MB的垂直平分线l交MA于点P，求动点P的轨迹方程．分析：根据题意画出图形，利用垂直平分线转换线段的关系得到PA+PB=4，据椭圆的定义即可得到动点P的轨迹方程．
解答：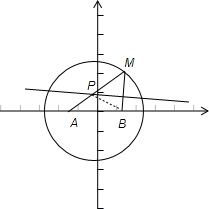
解：以线段AB的中点为坐标原点，
直线AB为x轴，线段AB的中点为原点，建立直角坐标系．
由垂直平分线知，PB=PM
故PA+PB=PM+PB=AM=4，
即P点的轨迹为以A、B为焦点的椭圆，中心为（0，0），
故P点的方程为
+
=1．
解：以线段AB的中点为坐标原点，直线AB为x轴，线段AB的中点为原点，建立直角坐标系．
由垂直平分线知，PB=PM
故PA+PB=PM+PB=AM=4，
即P点的轨迹为以A、B为焦点的椭圆，中心为（0，0），
故P点的方程为
| x2 |
| 4 |
| y2 |
| 3 |
点评：定义法：运用解析几何中一些常用定义（例如圆锥曲线的定义），可从曲线定义出发直接写出轨迹方程，或从曲线定义出发建立关系式，从而求出轨迹方程．
练习册系列答案
相关题目
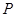满足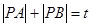
，若P点的轨迹是椭圆，则
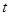的取值范围是
。