题目内容
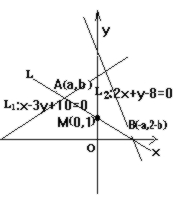
已知: 点M(0,1), 过M作一直线l, 使它夹在两已知直线l1:x - 3y + 10 ＝ 0和l2:2x + y - 8 ＝ 0间的线段被点M平分, 则直线l 的方程是_________.(用一般式表示)
答案：x+4y-4=0
解析：
解析：
|
解: 设l 交l1于点A, A(a,b) 则l 交l2于点B, B(-a,2-b) 从而 a - 3b + 10 ＝ 0 ① -2a - b - 6 ＝ 0 ② 解①,②得 b ＝ 2 a ＝ 6 - 10 ＝ -4 所以 A(-4,2), B(4,0) 从而l 的方程为 x + 4y - 4 ＝ 0
|
练习册系列答案
相关题目
-
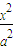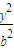=1（a＞b＞0）的离心率为
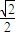，已知A（a，0），B（0，-b），且原点O到直线AB的距离为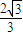
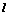，斜率为k，与圆C：(x-2)2+(y-3)2=1相交于M、N两个不同点
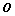为坐标原点，且
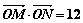，求k的值。