题目内容
(
华南师大附中模拟)已知函数 (x>0).
(x>0).
(1)
当0<a<b,且f(a)=f(b)时,求证:ab>1;(2)
是否存在实数a,b(a<b),使得函数y=f(x)的定义域、值域都是[a,b],若存在,则求出a,b的值;若不存在,请说明理由.
答案:略
解析:
解析:
|
解析: (1) 故f(x)在(0,1]上是减函数,而在 故f(x)在(0,1]上是减函数,而在 上是增函数,由0<a<b而f(a)=f(b)得0<a<1<b, 上是增函数,由0<a<b而f(a)=f(b)得0<a<1<b,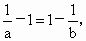 即 即 ,而 ,而 ,所以ab>1. ,所以ab>1.
(2) 不存在这样的实数a,b.假设存在这样的实数a,b使得函数y=f(x)的定义域、值域是都是[a,b],①当0<a<b<1时,函数 在(0,1]上是减函数,则 在(0,1]上是减函数,则 即 即 解得a=b,与0<a<b<1矛盾,故此时不存在满足条件的实数a,b. 解得a=b,与0<a<b<1矛盾,故此时不存在满足条件的实数a,b.
②当 1<a<b时,函数 在 在 上是增函数,则 上是增函数,则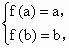 即 即 此时实数a,b为方程 此时实数a,b为方程 的两根,但方程 的两根,但方程 无实数根,因此不存在满足条件的实a,b. 无实数根,因此不存在满足条件的实a,b.
③当 0<a<1<b时,显然有 ,而 ,而 (这是因为a>0),故此时不存在满足条件的实数a,b. (这是因为a>0),故此时不存在满足条件的实数a,b.
综合①②③可得满足条件的实数是不存在的. |

练习册系列答案
相关题目
(
华南师大附中模拟)下列关系中,成立的是[
]|
A . |
B . |
|
C .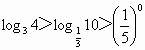 |
D . |
 ,则下列判断中正确的是
,则下列判断中正确的是
 的图象,可以把函数
的图象,可以把函数 的图象
的图象
 的值;
的值;