题目内容
已知公差不为零的等差数列的第4、7、16项分别是某等比数列的第4、6、8项,则该等比数列的公比为( )
A、
| ||
B、
| ||
C、±
| ||
D、±
|
分析:因为等差数列的第4、7、16项分别是某等比数列的第4、6、8项,得到a72=a4•a16,然后根据等差数列的通项公式分别求出这三项,解得a1=2d,求出第5项与第一项的比值得到公比q.
解答:解:由于等差数列{an}的公差d≠0,
它的第4、7、16项顺次成等比数列,
即a72=a4•a16,
也就是(a1+6d)2=(a1+3d)(a1+15d)?a1=-
d,
于是a4=a1+3d=
d,a7=a1+6d=
d,所以 q2=
=
=3.
∴q=±
故选C.
它的第4、7、16项顺次成等比数列,
即a72=a4•a16,
也就是(a1+6d)2=(a1+3d)(a1+15d)?a1=-
| 3 |
| 2 |
于是a4=a1+3d=
| 3 |
| 2 |
| 9 |
| 2 |
| a7 |
| a4 |
| ||
|
∴q=±
| 3 |
故选C.
点评:考查学生掌握等差数列通项公式,利用等比数列的性质来解决数学问题.属中档题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
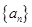 与公比为
与公比为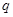 的等比数列
的等比数列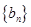 有相同的首项,同时满足
有相同的首项,同时满足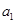 ,
,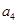 ,
,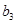 成等比,
成等比, ,
,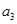 ,
,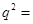 ( )
( )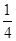 B.
B.
 C.
C.
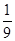 D.
D.