题目内容
 已知:α⊥β,α∩β=l,A∈α,B∈β,点A在直线l上的射影为A1,点B在l上的射影为B1,已知AB=2,AA1=1,BB1=
已知:α⊥β,α∩β=l,A∈α,B∈β,点A在直线l上的射影为A1,点B在l上的射影为B1,已知AB=2,AA1=1,BB1=| 2 |
求:二面角A1-AB-B1的大小的正弦值.
分析:因为BB1⊥α,利用线面垂直的判定定理可以得到平面ABB1⊥α,再利用三垂线定理根据二面角的定义求出二面角的平面角的平面角,在放到三角形中解出即可.
解答:解:∵BB1⊥α,∴平面ABB1⊥α.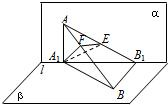
在平面α内过A1作A1E⊥AB1交AB1于E,则A1E⊥平面AB1B.过E作EF⊥AB交AB于F,连接A1F,则由三垂线定理得A1F⊥AB,
∴∠A1FE就是所求二面角的平面角.
在Rt△ABB1中,∠BAB1=45°,
∴AB1=B1B=
.
∴Rt△AA1B中,A1B=
=
=
.
由AA1•A1B=A1F•AB得A1F=
=
=
,
∴在Rt△A1EF中,sin∠A1FE=
=
,
∴二面角A1-AB-B1的正弦值为
.

在平面α内过A1作A1E⊥AB1交AB1于E,则A1E⊥平面AB1B.过E作EF⊥AB交AB于F,连接A1F,则由三垂线定理得A1F⊥AB,
∴∠A1FE就是所求二面角的平面角.
在Rt△ABB1中,∠BAB1=45°,
∴AB1=B1B=
| 2 |
∴Rt△AA1B中,A1B=
AB2-A
|
| 4-1 |
| 3 |
由AA1•A1B=A1F•AB得A1F=
| AA1•A1B |
| AB |
1×
| ||
| 2 |
| ||
| 2 |
∴在Rt△A1EF中,sin∠A1FE=
| A1E |
| A1F |
| ||
| 3 |
∴二面角A1-AB-B1的正弦值为
| ||
| 3 |
点评:本题主要考查了二面角的平面角 的有关知识,找出二面角的平面角是解题的难点和关键,一般利用三垂线定理找到二面角的平面角,再利用解三角形的有关知识求出二面角即可.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
某地区为下岗人员免费提供财会和计算机培训,以提高下岗人员的再就业能力.每名下岗人员可以选择参加一项培训、参加两项培训或不参加培训,已知参加过财会培训的有60%,参加过计算机培训的有75%.假设每个人对培训项目的选择是相互独立的,且各人的选择相互之间没有影响.
(Ⅰ)任选1名下岗人员,求该人参加过培训的概率;
(Ⅱ)任选3名下岗人员,记ξ为3人中参加过培训的人数,求ξ的分布列和期望.
(Ⅰ)任选1名下岗人员,求该人参加过培训的概率;
(Ⅱ)任选3名下岗人员,记ξ为3人中参加过培训的人数,求ξ的分布列和期望.
| ξ | 0 | 1 | 2 | 3 |
| P | 0.021 | 0.027 | 0.243 | 0.729 |
已知函数f(x)=-x3+ax2-x-1在(-∞,+∞)上是单调函数,则实数a的取值范围是( )
A、(-∞,-
| ||||
B、[-
| ||||
C、(-∞,-
| ||||
D、(-
|
已知函数f(x)=
若f(2-a2)>f(a),则实数a的取值范围是( )
|
| A、(-∞,-1)∪(2,+∞) |
| B、(-1,2) |
| C、(-2,1) |
| D、(-∞,-2)∪(1,+∞) |