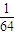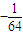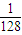题目内容
若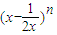
的展开式中第3项的二项式系数是15，则展开式中所有项系数之和为（ ）A．
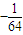
B．
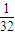
C．
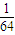
D．
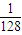
【答案】分析：根据题意，结合二项式定理可得Cn2=15，解可得n=6，将其代入二项式，并令x=1，计算（x-
）6的值，可得答案．
解答：解：由二项式定理，
的展开式中第3项的二项式系数是Cn2，
又由题意，其展开式中第3项的二项式系数是15，则Cn2=15，
解可得n=6，
在（x-
）6中，令x=1，可得其展开式中所有项系数之和为（
）6=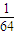
，
故选C．
点评：本题考查二项式系数的性质，要注意区分某一项的系数与某一项的二项式系数的区别，其次要掌握用特殊值法求二项式的展开式中所有项系数之和．
）6的值，可得答案．解答：解：由二项式定理，
的展开式中第3项的二项式系数是Cn2，又由题意，其展开式中第3项的二项式系数是15，则Cn2=15，
解可得n=6，
在（x-
）6中，令x=1，可得其展开式中所有项系数之和为（）6=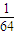，故选C．
点评：本题考查二项式系数的性质，要注意区分某一项的系数与某一项的二项式系数的区别，其次要掌握用特殊值法求二项式的展开式中所有项系数之和．
练习册系列答案
阅读快车系列答案
相关题目
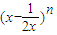的展开式中第3项的二项式系数是15，则展开式中所有项的系数之和为 ．
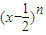的展开式中第3项的二项式系数是15，则展开式中所有项系数之和为（ ）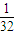
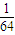
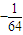
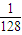
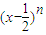的展开式中第3项的二项式系数是15，则展开式中所有项系数之和为（ ）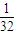
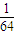
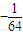
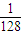
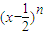的展开式中第3项的二项式系数是15，则展开式中所有项系数之和为（ ）
