题目内容
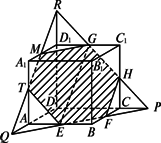
正方体是常见并且重要的多面体,对它的研究将有助于我们对立体几何一些概念的理解和掌握.如图所示,在正方体AC1中,E、F、G、H分别是所在棱的中点,请思考并回答下列问题:

(1)点E、F、G、H共面吗?
(2)直线EF、GH、DG能交于一点吗?
(3)若E、F、G、H四点共面,怎样才能画出过四点E、F、G、H的平面与正方体的截面?
(4)若正方形的棱长为a,那么(3)中的截面面积是多少?
答案:
解析:
解析:
|
解:(1)由平面的基本性质可知,要判断四点共面可以考虑由四点能构成相交直线或平行直线. 本问题中,可考虑证明EG∥FH. (2)思路一:要证三线共点,可先证两线共点,然后证明另一线也通过这一点. 因为E、F分别为棱AB、BC的中点,易得E、F∈面ABCD且EF与CD相交,设交点为P. 由△EBF≌△PCF可得PC=BE= 同理,GH与CD相交,设交点为P1,同样可得P1C=C1G= 所以P1与P重合,因此(2)得证.
思路二:要证三线共点,可先证某两线相交(如图中的EF、GH相交,设交点为P),然后证明P既在平面DCC1D1内又在平面ABCD内,从而由公理3可得P一定在两平面的交线CD上,于是可得三线共点. (3)作截面的关键在于作出截面与各个侧面的交线(或者是作出截面与正方体的各棱的交点),而要确定两个平面的交线,要找到同时在两个平面上的至少两个点.延长HG、DD1相交于点R,延长FE交DA延长线于Q,则点R、Q是截面与侧面AD1的公共点,连结RQ与A1D1、A1A分别交于点M、T,连结GM、TE,可得截面与正方体各面的交线分别为EF、FH、HG、GM、MT、TE.截面如图阴影部分所示. (4)截面为正六边形,其面积为 |

练习册系列答案
相关题目