题目内容
(08年赤峰二中模拟理) 已知正三棱柱ABC - A1B1C1中, AA1 = 2AC = 4, 延长CB至D, 使CB = BD.
(I)求证: 直线C1B // 平面AB1D;
(II)求平面AB1D与平面ACB所成角.

解析:法一: (Ⅰ) 因为 C1B1 = CB = DB, 且C1B1 // BD,
∴ 四边形C1BDB1是平行四边形,
∴ C1B // B1D,
又B1D Ì 平面AB1D,
∴ 直线C1B // 平面AB1D.
(Ⅱ) 过B1作B1H ^ AD于H, 连结BH.
∵ B1B ^ 平面ACD,
∴ BH ^ AD
∴ Ð B1HB是平面AB1D平面ACB所成角的平面角.
在△ACD中, 由于CB = BD = BA,
∴ ∠DAC = 90°,
∴ BH =![]() AC,
AC,
∵ AA1 = 2AC = 4,
∴ tanÐB1HB =![]() = 4,
= 4,
∴ 平面AB1D平面ACB所成角为arctan4.
法二: 在△ACD中, 由于CB = BD = BA,
∴ ∠DAC=90°,
如图, 以A为原点, 以AD为x轴正向, 建立空间直角坐标系O - xyz,
∵ 正三棱柱ABC - A1B1C1中, AA1 = 2AC = 4,
∴ A(0, 0, 0), B(![]() , 1, 0), B1(
, 1, 0), B1(![]() , 1, 4),
, 1, 4),
C1(0, 2, 4), D(2![]() , 0, 0).
, 0, 0).
(Ⅰ) ∵![]() = (-
= (-![]() , 1, 4),
, 1, 4),![]() = (-
= (-![]() , 1, 4),
, 1, 4),
∴![]() //
//![]()
又BC1 Ë 平面AB1D, B1D Ì 平面AB1D,
∴ 直线C1B // 平面AB1D.
(Ⅱ) ![]() =(2
=(2![]() , 0, 0),
, 0, 0), ![]() = (
= (![]() , 1, 4), 设平面AB1D的法向量n = (x, y, z), 则
, 1, 4), 设平面AB1D的法向量n = (x, y, z), 则
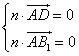 , 即
, 即 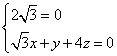 , ∴
, ∴ ![]() ,
,
取z = 1, 则n = (0, - 4, 1), 取平面ACB的法向量为m = (0, 0, 1),
则cos<n, m> =![]() ,
,



