题目内容
正方体ABCD-A1B1C1D1中,M为棱AB的中点,则异面直线DM与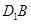 所成角的余弦值为()
所成角的余弦值为()
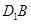 所成角的余弦值为()
所成角的余弦值为()A. | B.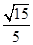 | C.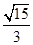 | D. |
B
试题分析:取CD的中点为N,连接BN,
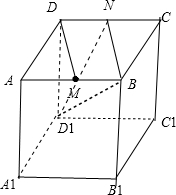
因为在正方体ABCD-A1B1C1D1中,M为棱AB的中点,
所以DM∥BN,
所以异面直线DM与D1B所成角等于直线BN与D1B所成角.
设正方体的棱长为2,所以D1N=
 ,BN=
,BN=  ,D1B="2"
,D1B="2" 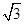 ,
,所以在△D1BN中,由余弦定理可得:cos∠D1BN=
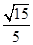 ,故选B.
,故选B.点评:解决该试题的关键是取CD的中点为N,连接BN,根据题意并且结合正方体的结构特征可得DM∥BN,所以异面直线DM与D1B所成角等于直线BN与D1B所成角或者其补角,再利用解三角形的有关知识求出答案

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 是矩形,
是矩形,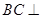 平面
平面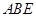 ,
,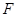 是
是 上一点,
上一点,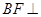 平面
平面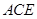 ,点
,点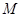 ,
,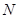 分别是
分别是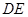 的中点.
的中点. 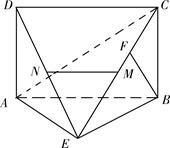
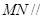 平面
平面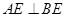 .
. 

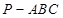 中,底面
中,底面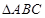 是边长为2的正三角形,
是边长为2的正三角形,  ⊥底面
⊥底面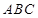 ,且
,且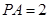 ,则此三棱锥外接球的半径为( )
,则此三棱锥外接球的半径为( )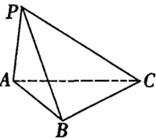
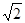

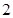
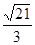
 的各棱长均为2,侧面
的各棱长均为2,侧面
 底面
底面 ,侧棱
,侧棱 与底面
与底面 .
. 与底面
与底面 上是否存在点
上是否存在点 ,使得平面
,使得平面 平面
平面 ?若存在,求出
?若存在,求出 的长;若不存在,请说明理由。
的长;若不存在,请说明理由。
 的边
的边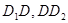 的中点,沿SE、SF、EF将它折成一个几何体,使
的中点,沿SE、SF、EF将它折成一个几何体,使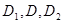 重合,记作D,给出下列位置关系:①SD
重合,记作D,给出下列位置关系:①SD 面EFD ; ②SE
面EFD ; ②SE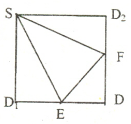
 轴上的三角形,采用斜二测画法作出其直观图,其直观图面积是原三角形面积的 ( )
轴上的三角形,采用斜二测画法作出其直观图,其直观图面积是原三角形面积的 ( ) 倍
倍 倍
倍 倍
倍