Question

集合S＝｛x｜x≤10，且x∈N^*｝，AS，BS，且A∩B＝｛4，5｝，(_SB)∩A＝｛1，2，3｝，(_SA)∩(_SB)＝｛6，7，8｝.求集合A和B.

 

Answer 1

答案：
解析：

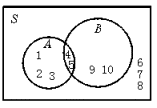
解法一：(1)∵A∩B＝｛4，5｝， ∴4∈A，5∈A，4∈B，5∈B (2)∵(SB)∩A＝｛1，2，3｝， ∴1∈A，2∈A，3∈A，1B，2B，3B. (3)∵(SA)∩(SB)＝｛6，7，8｝ ∴6、7、8都不属于A，6、7、8也都不属于B. ∵S＝｛x｜x≤10，且x∈N*｝，∴9、10不知所属。 由(2)、(3)可知9、10均不属于SB.∴9∈B，10∈B. 综上所述知A＝｛4，5，1，2，3｝，B＝｛4，5，9，10｝。 解法二： 如图所示 ∵A∩B＝｛4，5｝， ∴将4、5写在A∩B中， ∵(SB)∩A={1，2，3}， ∴将1，2，3写在A中。 ∵(SB)∩(SA)＝｛6，7，8｝， ∴将6，7，8写在S中A、B之外， ∵(SB)∩A与(SB)∩(SA)中均无9、10， ∴9、10在B中 故A＝｛1，2，3，4，5｝，B＝｛4，5，9，10｝。