题目内容
设f(x)是R上的奇函数,对任意实数x都有f(x+2)=-f(x),当-1≤x≤1时,f(x)=x3(1)求证:x=1是函数f(x)的一条对称轴
(2)证明函数f(x)是以4为周期的函数,并求x∈[1,5]时,f(x)的解析式.
【答案】分析:(1)直接根据f(x+2)=-f(x)=f(-x)对任意实数X成立即可得到结论;
(2)根据f(x+4)=-f(x+2)=-[-f(x)]=f(x)即可得到 f(x)是以4为最小正周期的周期函数;再结合对称轴以及周期即可求出x∈[1,5]时,f(x)的解析式.
解答:解:(1)证明:因为奇函数,所以f(x+2)=-f(x)=f(-x)对任意实数X成立.
又因为x+2,-x关于直线x=1对称,
故:直线x=1是函数f(x)图象上的一条对称轴
(2)证明:因为:f(x+2)=-f(x)
所以:f(x+4)=-f(x+2)=-[-f(x)]=f(x)
∴f(x)是以4为最小正周期的周期函数因为:直线x=1是函数f(x)图象上的一条对称轴;
所以:1≤x≤3的图象与-1≤x≤1的图象关于直线x=1对称.
故:f(x)=-(x-2)3,1≤x≤3;
∵f(x)是以4为最小正周期的周期函数
∴3≤x≤5的图象与-1≤x≤1的图象
∴f(x)=(x-4)3,3≤x≤5.
∴f(x)=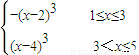 .
.
点评:本题主要考查了函数的周期性以及奇偶性,对称性.要特别利用好题中的关系式f(x+2)=-f(x).
(2)根据f(x+4)=-f(x+2)=-[-f(x)]=f(x)即可得到 f(x)是以4为最小正周期的周期函数;再结合对称轴以及周期即可求出x∈[1,5]时,f(x)的解析式.
解答:解:(1)证明:因为奇函数,所以f(x+2)=-f(x)=f(-x)对任意实数X成立.
又因为x+2,-x关于直线x=1对称,
故:直线x=1是函数f(x)图象上的一条对称轴
(2)证明:因为:f(x+2)=-f(x)
所以:f(x+4)=-f(x+2)=-[-f(x)]=f(x)
∴f(x)是以4为最小正周期的周期函数因为:直线x=1是函数f(x)图象上的一条对称轴;
所以:1≤x≤3的图象与-1≤x≤1的图象关于直线x=1对称.
故:f(x)=-(x-2)3,1≤x≤3;
∵f(x)是以4为最小正周期的周期函数
∴3≤x≤5的图象与-1≤x≤1的图象
∴f(x)=(x-4)3,3≤x≤5.
∴f(x)=
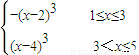 .
.点评:本题主要考查了函数的周期性以及奇偶性,对称性.要特别利用好题中的关系式f(x+2)=-f(x).

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目