题目内容
设函数f(x)=loga(x-3a)(a>0且a≠1),当点P(x,y)是函数y=f(x)图像上的点时,点Q(x-2a,-y)是函数y=g(x)图像上的点.
(1)写出函数y=g(x)的解析式;
(2)若当x∈[a+2,a+3]时,恒有|f(x)-g(x)|≤1,试确定a的取值范围.
(1) g(x)=loga![]() (2) a的取值范围是0<a≤
(2) a的取值范围是0<a≤![]()
解析:
(1)设点Q的坐标为(x′,y′),
则x′=x-2a,y′=-y. 即x=x′+2a,y=-y′.
∵点P(x,y)在函数y=loga(x-3a)的图像上,
∴-y′=loga(x′+2a-3a),即y′=loga![]() ,∴g(x)=loga
,∴g(x)=loga![]() .
.
(2)由题意得x-3a=(a+2)-3a=-2a+2>0;![]() =
=![]() >0,
>0,
又a>0且a≠1,∴0<a<1,
∵|f(x)-g(x)|=|loga(x-3a)-loga![]() |
|
=|loga(x2-4ax+3a2)|·|f(x)-g(x)|≤1,
∴-1≤loga(x2-4ax+3a2)≤1,
∵0<a<1,∴a+2>2a![]() f(x)=x2-4ax+3a2在[a+2,a+3]上为减函数,
f(x)=x2-4ax+3a2在[a+2,a+3]上为减函数,
∴μ(x)=loga(x2-4ax+3a2)在[a+2,a+3]上为减函数,
从而[μ(x)]max=μ(a+2)=loga(4-4a),[μ(x)]min=μ(a+3)=loga(9-6a),于是所求问题转化为求不等式组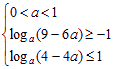 的解.
的解.
由loga(9-6a)≥-1解得0<a≤![]() ,
,
由loga(4-4a)≤1解得0<a≤![]() ,
,
∴所求a的取值范围是0<a≤![]() .
.

练习册系列答案
相关题目