题目内容
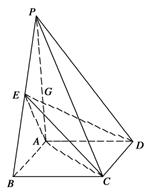
四棱锥(Ⅰ)证明:![]() ;
;
(Ⅱ)设侧面![]() 为等边三角形,求二面角
为等边三角形,求二面角![]() 的大小.
的大小.
解法一:
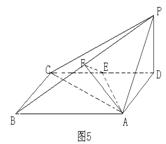
(Ⅰ)作AO⊥BC,垂足为O,连接OD,由题设知,AO⊥底面BCDE,且O为BC中点,
由![]() 知,Rt△OCD~Rt△CDE,从而∠ODC=∠CED,于是CE⊥OD.
知,Rt△OCD~Rt△CDE,从而∠ODC=∠CED,于是CE⊥OD.
由三垂线定理知,AD⊥CE.
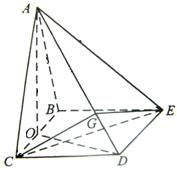
(Ⅱ)作CG⊥AD,垂足为G,连接GE。
由(Ⅰ)知,CE⊥AD,又CE![]() CG=C,
CG=C,
故AD⊥平面CGE,AD⊥GE,所以∠CGE是二面角C-AD-E的平面角。

解法二:
(Ⅰ)作AO⊥BC,垂足为O。
由题设知AO⊥底面BCDE,且O为BC的中点。
以O为坐标原点,射线OC为x轴正向,建立如图所示的直角坐标系O-xyz.
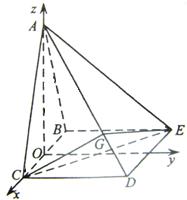
设A(0,0,t),由已知条件有
C(1,0,0), D(1, ![]() ,0),E(-1,
,0),E(-1, ![]() ,0),
,0),
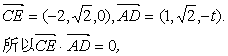
知AD⊥CE.
(Ⅱ)△ABC为等边三角形,因此A(0,0,![]() ).
).
作CG⊥AD,垂足为G,连接GE,在Rt△ACD中,求得|AG|=![]()
故![]()
![]()
![]()
![]()
所以![]() 与
与![]() 的夹角等于二面角C-AD-E的平面角.
的夹角等于二面角C-AD-E的平面角.

知二面角C-AD-E为arccos(![]() ).
).

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目

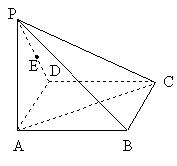
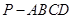 中,底面
中,底面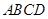 为矩形,侧棱
为矩形,侧棱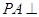 底面
底面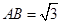 ,
,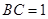 ,
, ,
,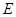 为
为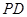 的中点.
的中点.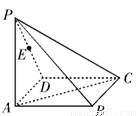
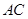 与
与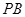 所成角的余弦值;
所成角的余弦值;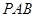 内找一点
内找一点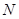 ,使
,使 面
面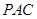 ,并求出
,并求出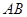 和
和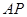 的距离.
的距离.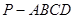 中,底面
中,底面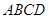 为矩形,
为矩形,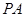 ⊥底面
⊥底面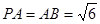 ,点
,点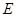 是棱
是棱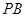 的中点.
的中点.
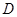 到平面
到平面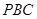 的距离;
的距离;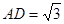 ,求二面角
,求二面角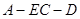 的平面角的余弦值 .
的平面角的余弦值 .