题目内容
(20)设a为实数,设函数(Ⅰ)设t=![]() ,求t的取值范围,并把f(x)表示为t的函数m(t)
,求t的取值范围,并把f(x)表示为t的函数m(t)
(Ⅱ)求g(a)
(Ⅲ)试求满足![]() 的所有实数a
的所有实数a
(20)本小题主要考查函数、方程等基本知识,考查分类讨论的数学思想方法和综合运用数学知识分析问题、解决问题的能力.
解:(Ⅰ)∵t=![]()
∴要使t有意义,必须1+x≥0且1-x≥0,即-1≤x≤1.
∵t2=2+2![]() t≥0, ①
t≥0, ①
∴t的取值范围是[![]() ].
].
由①得![]()
∴m(t)=a![]()
(Ⅱ)由题意知g(a)即为函数m(t)=![]() at2+t-a,t∈[
at2+t-a,t∈[![]() ,2]的最大值.
,2]的最大值.
注意到直线t=-![]() 是抛物线m(t)=
是抛物线m(t)=![]() at2+t-a的对称轴,分以下几种情况讨论.
at2+t-a的对称轴,分以下几种情况讨论.
(1)当a>0时,函数y=m(t),t∈[![]() ,2]的图像是开口向上的抛物线的一段,由t=-
,2]的图像是开口向上的抛物线的一段,由t=-![]() 知m(t)在[
知m(t)在[![]() ,2]上单调递增,
,2]上单调递增,
∴g(a)=m(2)=a+2.
(2)当a=0时,m(t)=t,t∈[![]() ,2],∴g(a)=2.
,2],∴g(a)=2.
(3)当a<0时,函数y=m(t),t∈[![]() ,2]的图像是开口向下的抛物线的一段.
,2]的图像是开口向下的抛物线的一段.
若t=-![]() ],即a≤-
],即a≤-![]() ,则g(a)=m(
,则g(a)=m(![]() )=
)=![]() .
.
若t=-![]() ],即a∈(-
],即a∈(-![]() ,-
,-![]() ),则g(a)=m(-
),则g(a)=m(-![]() )=-a-
)=-a-![]()
若t=-![]() ),即a∈(-
),即a∈(-![]() ,0),则g(a)=m(2)=a+2.
,0),则g(a)=m(2)=a+2.
综上有 g(a)=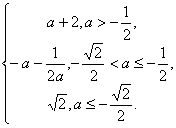
(Ⅲ)解法一:
情形1:当a<-2时,![]() 此时g(a)=
此时g(a)=![]() ,g(
,g(![]() )=
)=![]() +2.
+2.
由2+![]() =
=![]() 解得a=-1-
解得a=-1-![]() ,与a<-2矛盾.
,与a<-2矛盾.
情形2:当-2≤a<-![]() 时,-
时,-![]() <
<![]() ,此时g(a)=
,此时g(a)=![]() ,
,
g(![]() )=-
)=-![]() -
-![]() ,由
,由![]() =-
=-![]() -
-![]() 解得a=-
解得a=-![]() ,与a<-
,与a<-![]() 矛盾.
矛盾.
情形3:当-![]() ≤a≤-
≤a≤-![]() 时,-
时,-![]() ≤
≤![]() ≤-
≤-![]() ,此时g(a)=
,此时g(a)=![]() =g(
=g(![]() ),
),
所以-![]() ≤a≤-
≤a≤-![]() .
.
情形4:当-![]() <a≤-
<a≤-![]() 时,-2≤
时,-2≤![]() <-
<-![]() ,此时g(a)=-a-
,此时g(a)=-a-![]()
g(![]() )=
)=![]() ,由-a-
,由-a-![]() 解得a=-
解得a=-![]() ,与a>-
,与a>-![]() 矛盾.
矛盾.
情形5:当-![]() <a<0时,
<a<0时,![]() <-2,此时g(a)=a+2,g(
<-2,此时g(a)=a+2,g(![]() )=
)=![]() ,
,
由a+2=![]() 解得a=
解得a=![]() -2,与a>-
-2,与a>-![]() 矛盾.
矛盾.
情形6:当a>0时,![]() >0,此时g(a)=a+2,g(
>0,此时g(a)=a+2,g(![]() )=
)=![]() +2,
+2,
由a+2=![]() +2解得a=±1,由a>0知a=1.
+2解得a=±1,由a>0知a=1.
综上知,满足g(a)=g(![]() )的所有实数a为:
)的所有实数a为:
-![]() ≤a≤-
≤a≤-![]() 或a=1.
或a=1.
解法二:
当a>-![]() 时,g(a)=a+2>
时,g(a)=a+2>![]()
当-![]() <a≤-
<a≤-![]() 时,-a∈[
时,-a∈[![]() -
-![]() ],所以-a≠-
],所以-a≠-![]()
g(a)=-a-![]() >2
>2![]() 因此,当a>-
因此,当a>-![]() 时,g(a)>
时,g(a)>![]() .
.
当a>0时,![]() >0,由g(a)=g(
>0,由g(a)=g(![]() )知a+2=
)知a+2=![]() +2解得a=1.
+2解得a=1.
当a<0时,a·![]() =1,因此a≤-1或
=1,因此a≤-1或![]() ≤-1,从而g(a)=
≤-1,从而g(a)=![]() 或g(
或g(![]() )=
)=![]() .
.
要使g(a)=g(![]() ),必须有a≤-
),必须有a≤-![]() ,
,![]() ≤-
≤-![]() ,即-
,即-![]() ≤a≤-
≤a≤-![]() .
.
此时g(a)=![]() =g(
=g(![]() ).
).
综上知,满足g(a)=g(![]() )的所有实数a为:
)的所有实数a为:
-![]() ≤a≤-
≤a≤-![]() 或a=1.
或a=1.

 (选做题)在A,B,C,D四小题中只能选做2题,每小题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
(选做题)在A,B,C,D四小题中只能选做2题,每小题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.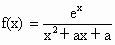 ,其中a为实数.
,其中a为实数.