题目内容
 如图,点A,B的坐标分别为(1,4)和(4,4),抛物线y=a(x-m)2+n的顶点在线段AB上运动(抛物线随顶点一起平移),与x轴交于C、D两点(C在D的左侧),点
如图,点A,B的坐标分别为(1,4)和(4,4),抛物线y=a(x-m)2+n的顶点在线段AB上运动(抛物线随顶点一起平移),与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则点D的横坐标最大值为( )
| A、-3 | B、1 | C、5 | D、8 |
分析:由题意可知:a<0,1≤m≤4,抛物线的最大值为4,可得n=4.当顶点取(1,4)时,点C取得最小值-3,得到0=a(-3-1)2+4,解得a=-
.于是y=-
(x-m)2+4.当顶点取(4,4)时,点D取得最大值,得到0=-
(x-4)2+4,解得x即可.
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
解答:解:由题意可知:a<0,1≤m≤4,抛物线的最大值为4,即n=4.
当顶点取(1,4)时,点C取得最小值-3,
∴0=a(-3-1)2+4,解得a=-
.
∴y=-
(x-m)2+4,
当顶点取(4,4)时,点D取得最大值,
∴0=-
(x-4)2+4,解得x=8或0.
把x=0舍去,故点D的横坐标最大值为8.
故选:D.
当顶点取(1,4)时,点C取得最小值-3,
∴0=a(-3-1)2+4,解得a=-
| 1 |
| 4 |
∴y=-
| 1 |
| 4 |
当顶点取(4,4)时,点D取得最大值,
∴0=-
| 1 |
| 4 |
把x=0舍去,故点D的横坐标最大值为8.
故选:D.
点评:本题考查了二次函数的图象与性质,属于难题.

练习册系列答案
相关题目
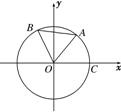 如图,点A,B是单位圆上的两点,A,B点分别在第一、二象限,点C是圆与x轴正半轴的交点,△AOB是正三角形,若点A的坐标为(
如图,点A,B是单位圆上的两点,A,B点分别在第一、二象限,点C是圆与x轴正半轴的交点,△AOB是正三角形,若点A的坐标为(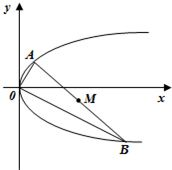 如图,过抛物线y2=2px(p>0)的顶点作两条互相垂直的弦OA、OB.
如图,过抛物线y2=2px(p>0)的顶点作两条互相垂直的弦OA、OB. 如图,点A、B分别是椭圆长轴的左、右端点,点F是椭圆的右焦点,其中A(-6,0),F(4,0),点P在椭圆上且位于x轴上方,
如图,点A、B分别是椭圆长轴的左、右端点,点F是椭圆的右焦点,其中A(-6,0),F(4,0),点P在椭圆上且位于x轴上方, 如图,点A、B为椭圆
如图,点A、B为椭圆