题目内容
在海岸A处,发现北偏东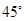 方向,距离A为
方向,距离A为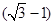 海里的B处有一走私船,在A北偏西
海里的B处有一走私船,在A北偏西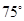 方向距离A为2海里的C处有我方一艘缉私艇奉命以
方向距离A为2海里的C处有我方一艘缉私艇奉命以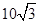 海里/小时的速度追截走私船,且C在B的正西方,此时走私船正以
海里/小时的速度追截走私船,且C在B的正西方,此时走私船正以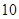 海里/小时的速度从B处向北偏东
海里/小时的速度从B处向北偏东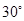 方向逃窜,问缉私艇沿什么方向,才能最快追上走私船?需要多长时间?
方向逃窜,问缉私艇沿什么方向,才能最快追上走私船?需要多长时间?
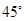 方向,距离A为
方向,距离A为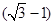 海里的B处有一走私船,在A北偏西
海里的B处有一走私船,在A北偏西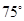 方向距离A为2海里的C处有我方一艘缉私艇奉命以
方向距离A为2海里的C处有我方一艘缉私艇奉命以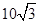 海里/小时的速度追截走私船,且C在B的正西方,此时走私船正以
海里/小时的速度追截走私船,且C在B的正西方,此时走私船正以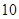 海里/小时的速度从B处向北偏东
海里/小时的速度从B处向北偏东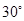 方向逃窜,问缉私艇沿什么方向,才能最快追上走私船?需要多长时间?
方向逃窜,问缉私艇沿什么方向,才能最快追上走私船?需要多长时间?若在D处相遇,则可先在△ABC中求出BC,再在△BCD中求∠BCD.
设缉私船用t h在D处追上走私船,则有CD=10 t,BD=10t.在△ABC中,
t,BD=10t.在△ABC中,
∵AB= -1,AC=2,∠BAC=120°,∴由余弦定理,得BC
-1,AC=2,∠BAC=120°,∴由余弦定理,得BC =AB
=AB +AC
+AC -2AB•AC•cos∠BAC
-2AB•AC•cos∠BAC
=( -1)
-1) +2
+2 -2×(
-2×( -1)×2×cos120°=6,
-1)×2×cos120°=6,
∴BC=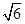 ,∵∠CBD=90°+30°=120°,在△BCD中,由正弦定理,得
,∵∠CBD=90°+30°=120°,在△BCD中,由正弦定理,得
sin∠BCD= ,,∴∠BCD=30°.
,,∴∠BCD=30°.
即缉私船北偏东60°方向能最快追上走私船.
设缉私船用t h在D处追上走私船,则有CD=10
 t,BD=10t.在△ABC中,
t,BD=10t.在△ABC中,∵AB=
 -1,AC=2,∠BAC=120°,∴由余弦定理,得BC
-1,AC=2,∠BAC=120°,∴由余弦定理,得BC =AB
=AB +AC
+AC -2AB•AC•cos∠BAC
-2AB•AC•cos∠BAC=(
 -1)
-1) +2
+2 -2×(
-2×( -1)×2×cos120°=6,
-1)×2×cos120°=6,∴BC=
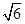 ,∵∠CBD=90°+30°=120°,在△BCD中,由正弦定理,得
,∵∠CBD=90°+30°=120°,在△BCD中,由正弦定理,得sin∠BCD=
 ,,∴∠BCD=30°.
,,∴∠BCD=30°.即缉私船北偏东60°方向能最快追上走私船.
可先在△ABC中求出BC,再在△BCD中求∠BCD

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
 内接于单位圆,且
内接于单位圆,且 ,则长为
,则长为 的三条线段( )
的三条线段( )
 中,
中,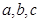 分别为内角
分别为内角 的对边,且
的对边,且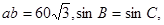 △
△ ,求边
,求边 的长.
的长. ,且
,且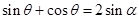 ,
, ,
,
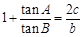 .
. ,n
,n ,试求|m
,试求|m n|的最小值.
n|的最小值.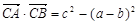 .
.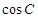 的值; (2) 若
的值; (2) 若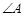 是钝角,求sinB的取值范围
是钝角,求sinB的取值范围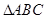 中,
中, ,则
,则 =( )
=( )



 ,
,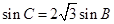 ,求A
,求A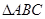 中,a,b,c分别是角A,B,C的对边,向量
中,a,b,c分别是角A,B,C的对边,向量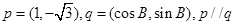 且
且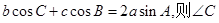 =( )
=( )


