题目内容
设关于x的不等式ax+b＞0的解集为{x|x＜1}，则关于x的不等式
＞0的解集为
| ax+b | x2-5x-6 |
{x|x＜-1或1＜x＜6}
{x|x＜-1或1＜x＜6}
．分析：依题意可知a+b=0且a＜0，利用标根法即可求得答案．
解答：解：∵不等式ax+b＞0的解集为{x|x＜1}，
∴1是方程ax+b=0的解，且a＜0，
∴a+b=0（a＜0），
∴
＞0?
＞0?
＜0，
由标根法得x＜-1或1＜x＜6．
∴原不等式的解集为：{x|x＜-1或1＜x＜6}．
故答案为：{x|x＜-1或1＜x＜6}．
∴1是方程ax+b=0的解，且a＜0，
∴a+b=0（a＜0），
∴
| ax+b |
| x2-5x-6 |
| a(x-1) |
| (x-6)(x+1) |
| (x-1) |
| (x-6)(x+1) |
由标根法得x＜-1或1＜x＜6．
∴原不等式的解集为：{x|x＜-1或1＜x＜6}．
故答案为：{x|x＜-1或1＜x＜6}．
点评：本题考查高次不等式的解法，着重考查标根法的应用，求得b=-a＞0是解决问题的基础，属于中档题．
练习册系列答案
相关题目
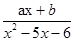＞0的解集为________.