题目内容
设平面α∥平面β，A∈α，B∈β，C是AB的中点，当A、B分别在α、β内运动时，那么所有的动点C
- A.不共面
- B.当且仅当A，B在两条相交直线上移动时才共面
- C.当且仅当A，B在两条给定的平行直线上移动时才共面
- D.不论A，B如何移动都共面
D
分析：本题考查空间想象力，因为平面α∥平面β，所以线段AB的中点到平面α和平面β的距离相等，从而动点C构成的图形是到平面α和平面β的距离相等的一个平面．
解答：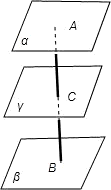
解：根据平行平面的性质，
不论A、B如何运动，
动点C均在过C且与α，β都平行的平面上．
故选：D
点评：本小题主要考查平面的基本性质及推论、确定平面的条件、共面的证明方法等基础知识，考查空间想象力、化归与转化思想．属于基础题．
分析：本题考查空间想象力，因为平面α∥平面β，所以线段AB的中点到平面α和平面β的距离相等，从而动点C构成的图形是到平面α和平面β的距离相等的一个平面．
解答：
解：根据平行平面的性质，不论A、B如何运动，
动点C均在过C且与α，β都平行的平面上．
故选：D
点评：本小题主要考查平面的基本性质及推论、确定平面的条件、共面的证明方法等基础知识，考查空间想象力、化归与转化思想．属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
α，点b∈β，则在β内过点b的所有直线中
l.又AB∩l=R,如图所示,设A、B、C三点确定的平面为γ,则β∩γ是（ ） 
α⊥β;
平面α⊥平面ABC;
l⊥平面ABC;
l∥平面ABC.