题目内容
(A组)关于x的不等式ax2+bx+c>0的解集为(-1,2),则不等式cx2+bx+a<0的解集为______.
(B组)关于x的不等式ax2+bx+2>0的解集为(-1,2),则a+b=______.
(B组)关于x的不等式ax2+bx+2>0的解集为(-1,2),则a+b=______.
(A组)∵关于x的不等式ax2+bx+c>0的解集为(-1,2),
∴-1和2为方程ax2+bx+c>0的两个实根,且a<0,
由韦达定理可得
,解得
,
故不等式cx2+bx+a<0可化为-2ax2-ax+a<0,(a<0)
即2x2+x-1<0,故(x+1)(2x-1)<0,
解得-1<x<
,故解集为{x|-1<x<
};
(B组)∵关于x的不等式ax2+bx+2>0的解集为(-1,2),
∴-1和2为方程ax2+bx+2>0的两个实根,且a<0,
由韦达定理可得
,解得
,
故a+b=0,
故答案为:{x|-1<x<
},0
∴-1和2为方程ax2+bx+c>0的两个实根,且a<0,
由韦达定理可得
|
|
故不等式cx2+bx+a<0可化为-2ax2-ax+a<0,(a<0)
即2x2+x-1<0,故(x+1)(2x-1)<0,
解得-1<x<
| 1 |
| 2 |
| 1 |
| 2 |
(B组)∵关于x的不等式ax2+bx+2>0的解集为(-1,2),
∴-1和2为方程ax2+bx+2>0的两个实根,且a<0,
由韦达定理可得
|
|
故a+b=0,
故答案为:{x|-1<x<
| 1 |
| 2 |

练习册系列答案
相关题目
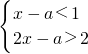 的解集为A.
的解集为A.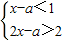 的解集为A.
的解集为A.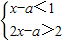 的解集为A.
的解集为A.