题目内容
已知m,n是空间两条不同的直线,α,β,γ是三个不同的平面,则下列命题正确的是( )
分析:A中,根据面面平行的性质知两平面内直线平行或异面;B中,可举一反例;据面面垂直的性质即可作出判断;利用线面平行的性质及线面垂直的判定定理即可证明;
解答:解:A中,由α∥β,m?α,n?β,可知m,n无公共点,则m,n平行或异面,故A错误;
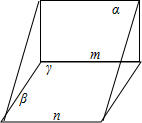
B中,如图所示:α∩γ=m,β∩γ=n,m∥n,但α与β相交,故B错误;
C中,设α∩β=n,由a⊥β,m?β,根据面面垂直性质知,若m⊥n,则m⊥α,否则m不垂直α;
D中,由m∥α知,过m可作平面γ交α于p,据线面平行的性质得m∥p,因为m⊥β,所以p⊥β,又p?α,所以α⊥β,故D正确;
故选D.
B中,如图所示:α∩γ=m,β∩γ=n,m∥n,但α与β相交,故B错误;

C中,设α∩β=n,由a⊥β,m?β,根据面面垂直性质知,若m⊥n,则m⊥α,否则m不垂直α;
D中,由m∥α知,过m可作平面γ交α于p,据线面平行的性质得m∥p,因为m⊥β,所以p⊥β,又p?α,所以α⊥β,故D正确;
故选D.
点评:本题以命题为载体,考查空间线面平行、垂直的性质定理、判定定理,考查空间两平面平行、垂直的性质及判定,考查学生的空间想象能力、逻辑推理能力.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 是三个不同的平面,则下列命题正确的是
是三个不同的平面,则下列命题正确的是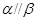 ,
,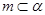 ,
,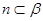 ,则
,则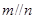 B.若
B.若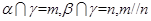 ,则
,则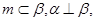 则
则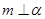 D.若
D.若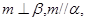 则
则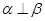
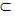 β,则下列命题为真命题的是
β,则下列命题为真命题的是