题目内容
(本题满分18分,第1小题6分,第2小题6分,第3小题6分)
对于定义在D上的函数 ,若同时满足
,若同时满足
(Ⅰ)存在闭区间 ,使得任取
,使得任取 ,都有
,都有 是常数);
是常数);
(Ⅱ)对于D内任意 ,当
,当 时总有
时总有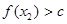 ,则称
,则称 为“平底型”函数。
为“平底型”函数。
(1)判断 是否是“平底型”函数?简要说明理由;
是否是“平底型”函数?简要说明理由;
(2)设 是(1)中的“平底型”函数,若
是(1)中的“平底型”函数,若 ,对一切
,对一切 恒成立,求实数
恒成立,求实数 的范围;
的范围;
(3)若 是“平底型”函数,求
是“平底型”函数,求 和
和 满足的条件,并说明理由。
满足的条件,并说明理由。
【答案】
【解析】解:(1)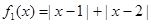 是“平底型”函数, ………………1分
是“平底型”函数, ………………1分
存在区间[1,2]使得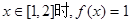 ,
,
当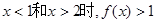 恒成立; ………………2分
恒成立; ………………2分
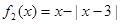 不是“平底型”函数, ………………1分
不是“平底型”函数, ………………1分
不存在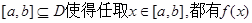 =常数 ………………1分
=常数 ………………1分
(2)若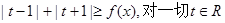 恒成立
恒成立
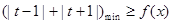
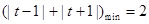 ………………3分
………………3分
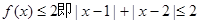
解得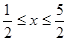 ………………3分
………………3分
(3)
(1)当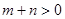 时
时
若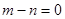 时,由图1b知,是“平底型”函数,存在[1,2]使
时,由图1b知,是“平底型”函数,存在[1,2]使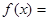 常数 …………1分
常数 …………1分
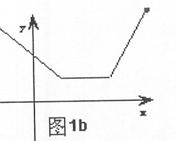
若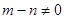 时,由图1a知,是“平底型”函数,存在[a,b]满足条件
…………1分
时,由图1a知,是“平底型”函数,存在[a,b]满足条件
…………1分
(2)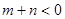 不是由图2知,不是“平底型”函数, …………1分
不是由图2知,不是“平底型”函数, …………1分
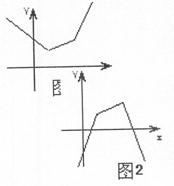
(3)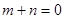 若
若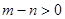 时,由图3知不是“平底型”函数,因为不存在区间[a,b]满足条件……1分
时,由图3知不是“平底型”函数,因为不存在区间[a,b]满足条件……1分
若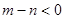 时,由图4知不是“平底型”函数,因为不存在区间[a,b]满足条件 …………1分
时,由图4知不是“平底型”函数,因为不存在区间[a,b]满足条件 …………1分
若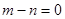 时,
时, ,显然不是“平底型”函数 ………………1分
,显然不是“平底型”函数 ………………1分


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,如果存在一个正整数
,如果存在一个正整数 ,使得对任意的
,使得对任意的 (
( )都有
)都有 成立,那么就把这样一类数列
成立,那么就把这样一类数列 时
时 的周期数列,当
的周期数列,当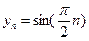 时
时 是周期为
是周期为 的周期数列。
的周期数列。 满足
满足 (
( (
( 不同时为0),且数列
不同时为0),且数列 的周期数列,求常数
的周期数列,求常数 的值;
的值; ,且
,且 .
. ,试判断数列
,试判断数列 ,试判断数列
,试判断数列 (
( ,
,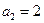 ,
, ,数列
,数列 的前
的前 ,使对任意的
,使对任意的 成立,若存在,求出
成立,若存在,求出 ,如果存在一个正整数
,如果存在一个正整数 ,使得对任意的
,使得对任意的 (
( )都有
)都有 成立,那么就把这样一类数列
成立,那么就把这样一类数列 时
时 的周期数列,当
的周期数列,当 时
时 是周期为
是周期为 的周期数列。
的周期数列。 满足
满足 (
( (
(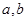 不同时为0),且数列
不同时为0),且数列 的周期数列,求常数
的周期数列,求常数 的值;
的值; ,且
,且 .
.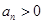 ,试判断数列
,试判断数列 ,试判断数列
,试判断数列 (
(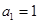 ,
,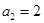 ,
, ,数列
,数列 的前
的前 ,使对任意的
,使对任意的 成立,若存在,求出
成立,若存在,求出 ,其中
,其中 .
. 时,设
时,设 ,
, ,求
,求 的解析式及定义域;
的解析式及定义域; 时,求
时,求 的最小值;
的最小值; ,当
,当 时,
时, 对任意
对任意 恒成立,求
恒成立,求 的取值范围.
的取值范围. 是等差数列,且公差为
是等差数列,且公差为 ,若数列
,若数列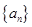 中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”.
中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”. ,求证:该数列是“封闭数列”;
,求证:该数列是“封闭数列”; 是否是“封闭数列”,为什么?
是否是“封闭数列”,为什么? 是数列
是数列 项和,若公差
项和,若公差 ,试问:是否存在这样的“封闭数列”,使
,试问:是否存在这样的“封闭数列”,使 ;若存在,求
;若存在,求