题目内容
附加题:
已知定义域为(-∞,0)∪(0,+∞)的偶函数g(x)在(-∞,0)内为单调递减函数,且g(x•y)=g(x)+g(y)对任意的x,y都成立,g(2)=1.
(1)求g(4),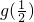 的值;
的值;
(2)求满足条件g(x)-2>g(x+1)的x的取值范围.
解:(1)∵g(x•y)=g(x)+g(y)对任意的x,y都成立,g(2)=1.
令x=y=2时有g(4)=g(2×2)=g(2)+g(2)=2
令x=y=1,可得g(1)=2g(1)∴g(1)=0
令x=2,y= 可得g(1)=g(2)+g(
可得g(1)=g(2)+g( )∴
)∴
(2)∵g(x)-2>g(x+1)
∴g(x)>2+g(x+1)=g(4)+g(x+1)=g[4(x+1)]
又∵g(x)为偶函数,且g(x)在(-∞,0)为单调递减函数,
∴g(x)在(0,+∞)为单调递增函数.
|x|>4|x+1|,|x+1|≠0
两边同时平方化简可得,15x2+32x+16<0
解二次不等式可得, 且x≠-1
且x≠-1
综上x的取值范围为
分析:(1)由g(x•y)=g(x)+g(y)对任意的x,y都成立及g(2)=1,考虑利用赋值法,取x=y=2可求g(4);要求g( ),可同样利用赋值法先求g(1),进而结合g(2)的值求g(
),可同样利用赋值法先求g(1),进而结合g(2)的值求g( )
)
(2)g(x)-2>g(x+1)?g(x)>g(x+1)+2,结合(1)及已知可以化简为g(x)>g[4(x+1)],g(x)为偶函数,且在(-∞,0)为单调递减函数,可得g(x)在(0,+∞)为单调递增函数.从而可得|x|>4|x+1|,|x+1|≠0,解不等式可求
点评:本题主要考查了利用赋值法求解抽象函数的函数值,还考查了偶函数的性质:对称区间上的单调性相反的性质的应用,解决本题的关键是由偶函数y=g(x)在(0,+∞)单调递增,g(a)>g(b)可|a|>|b|,考生容易漏洞由偶函数y=g(x)在(-∞,0)单调递减,从而误写为a>b.
令x=y=2时有g(4)=g(2×2)=g(2)+g(2)=2
令x=y=1,可得g(1)=2g(1)∴g(1)=0
令x=2,y=
 可得g(1)=g(2)+g(
可得g(1)=g(2)+g( )∴
)∴
(2)∵g(x)-2>g(x+1)
∴g(x)>2+g(x+1)=g(4)+g(x+1)=g[4(x+1)]
又∵g(x)为偶函数,且g(x)在(-∞,0)为单调递减函数,
∴g(x)在(0,+∞)为单调递增函数.
|x|>4|x+1|,|x+1|≠0
两边同时平方化简可得,15x2+32x+16<0
解二次不等式可得,
 且x≠-1
且x≠-1综上x的取值范围为

分析:(1)由g(x•y)=g(x)+g(y)对任意的x,y都成立及g(2)=1,考虑利用赋值法,取x=y=2可求g(4);要求g(
 ),可同样利用赋值法先求g(1),进而结合g(2)的值求g(
),可同样利用赋值法先求g(1),进而结合g(2)的值求g( )
) (2)g(x)-2>g(x+1)?g(x)>g(x+1)+2,结合(1)及已知可以化简为g(x)>g[4(x+1)],g(x)为偶函数,且在(-∞,0)为单调递减函数,可得g(x)在(0,+∞)为单调递增函数.从而可得|x|>4|x+1|,|x+1|≠0,解不等式可求
点评:本题主要考查了利用赋值法求解抽象函数的函数值,还考查了偶函数的性质:对称区间上的单调性相反的性质的应用,解决本题的关键是由偶函数y=g(x)在(0,+∞)单调递增,g(a)>g(b)可|a|>|b|,考生容易漏洞由偶函数y=g(x)在(-∞,0)单调递减,从而误写为a>b.

练习册系列答案
相关题目
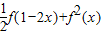 的值.
的值.