题目内容
在△ABC中,若c4-2(a2+b2)c2+a4+a2b2+b4=0,则∠C等于( )
A.90° B.120°
C.60° D.120°或60°
【答案】
D
【解析】
试题分析:由c4-2(a2+b2)c2+a4+a2b2+b4=0,得(a2+b2)2-2(a2+b2)c2+c4=a2b2,
∴ (a2+b2-c2)2=a2b2,
∴ a2+b2-c2=±ab,
∴ cosC=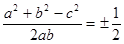 ,
,
∴ ∠C=120°或∠C=60°.故选D。
考点:本题主要考查余弦定理、代数式恒等变形。
点评:从c4-2(a2+b2)c2+a4+a2b2+b4=0出发,变换出a2+b2-c2=±ab,便于应用余弦定理。

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
在△ABC中,若c4-2(a2+b2)c2+a4+a2b2+b4=0,则∠C等于( )
| A、90° | B、120° | C、60° | D、120°或60° |