题目内容
已知⊙C:(x-3)2+(y-3)2=4,直线l:y=kx+1
(1)若l与⊙C相交,求k的取值范围;
(2)若l与⊙C交于A、B两点,且|AB|=2,求l的方程.
解:(1)∵⊙C与l相交,∴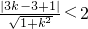 …(3分)
…(3分)
解得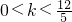 …(6分)
…(6分)
(2)∵圆半径r=2,|AB|=2,∴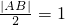 .
.
圆心到直线l的距离为d,则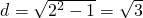 …(9分)
…(9分)
又由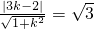 解得
解得 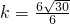 ,
,
故所求直线方程为: ,或
,或 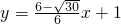 .
.
即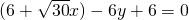 或
或 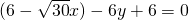 . …(12分)
. …(12分)
分析:(1)由于⊙C与l相交,故圆心到直线的距离小于半径,即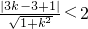 ,解不等式求得k的取值范围.
,解不等式求得k的取值范围.
(2)根据弦长公式求得圆心到直线l的距离d,再根据弦长公式求出d,由这两个d的值相等,解出k的值,即得所求
的直线方程.
点评:本题考查直线和圆的位置关系,点到直线的距离公式,弦长公式的应用,属于中档题.
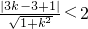 …(3分)
…(3分)解得
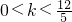 …(6分)
…(6分)(2)∵圆半径r=2,|AB|=2,∴
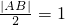 .
.圆心到直线l的距离为d,则
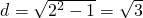 …(9分)
…(9分)又由
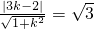 解得
解得 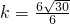 ,
,故所求直线方程为:
 ,或
,或 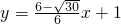 .
.即
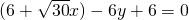 或
或 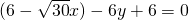 . …(12分)
. …(12分)分析:(1)由于⊙C与l相交,故圆心到直线的距离小于半径,即
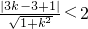 ,解不等式求得k的取值范围.
,解不等式求得k的取值范围.(2)根据弦长公式求得圆心到直线l的距离d,再根据弦长公式求出d,由这两个d的值相等,解出k的值,即得所求
的直线方程.
点评:本题考查直线和圆的位置关系,点到直线的距离公式,弦长公式的应用,属于中档题.

练习册系列答案
 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目