题目内容
函数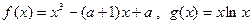
(Ⅰ)若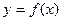 ,
,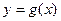 在
在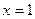 处的切线相互垂直,求这两个切线方程.
处的切线相互垂直,求这两个切线方程.
(Ⅱ)若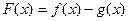 单调递增,求
单调递增,求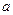 的范围.
的范围.
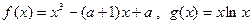
(Ⅰ)若
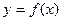 ,
,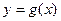 在
在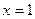 处的切线相互垂直,求这两个切线方程.
处的切线相互垂直,求这两个切线方程.(Ⅱ)若
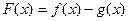 单调递增,求
单调递增,求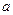 的范围.
的范围.(I)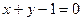 ,
,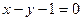 (II)
(II)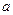 的范围为
的范围为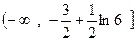
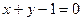 ,
,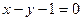 (II)
(II)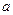 的范围为
的范围为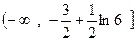
(I)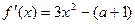 ,
, 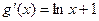 网w。w-w*k&s%5¥u
网w。w-w*k&s%5¥u
∴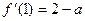
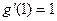
∵两曲线在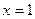 处的切线互相垂直
处的切线互相垂直
∴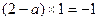 ∴
∴ 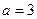
∴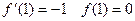 ∴
∴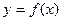 在
在 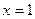 处的切线方程为
处的切线方程为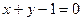 ,
,
同理,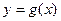 在
在 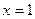 处的切线方程为
处的切线方程为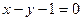 ………………6分
………………6分
(II) 由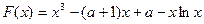
得 ……………8分
……………8分
∵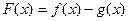 单调递增 ∴
单调递增 ∴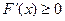 恒成立
恒成立
即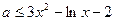 ……………10分
……………10分
令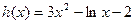 网w。w-w*k&s%5¥u
网w。w-w*k&s%5¥u
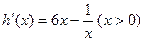 令
令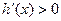 得
得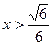 ,令
,令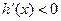 得
得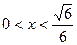
∴
∴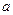 的范围为
的范围为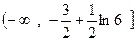 ……………13分
……………13分
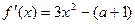 ,
, 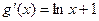 网w。w-w*k&s%5¥u
网w。w-w*k&s%5¥u∴
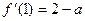
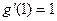
∵两曲线在
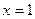 处的切线互相垂直
处的切线互相垂直 ∴
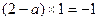 ∴
∴ 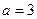
∴
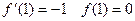 ∴
∴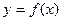 在
在 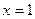 处的切线方程为
处的切线方程为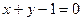 ,
, 同理,
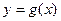 在
在 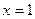 处的切线方程为
处的切线方程为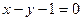 ………………6分
………………6分(II) 由
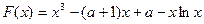
得
 ……………8分
……………8分∵
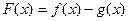 单调递增 ∴
单调递增 ∴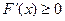 恒成立
恒成立即
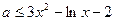 ……………10分
……………10分令
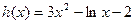 网w。w-w*k&s%5¥u
网w。w-w*k&s%5¥u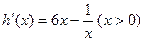 令
令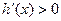 得
得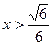 ,令
,令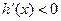 得
得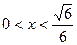
∴

∴
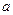 的范围为
的范围为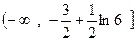 ……………13分
……………13分
练习册系列答案
相关题目
 上的函数
上的函数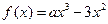 ,其中
,其中 为大于零的常数.
为大于零的常数.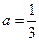 时,令
时,令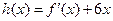 ,
, 时,
时, (
( 为自然对数的底数);
为自然对数的底数); ,在
,在 处取得最大值,
处取得最大值, (b、c、d为常数),当
(b、c、d为常数),当 时,
时, 只有一个实根,当
只有一个实根,当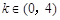 时,
时, 有2个极值点;②函数
有2个极值点;②函数 有一个相同的实根;④
有一个相同的实根;④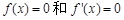 有一个相同的实根。
有一个相同的实根。 是一个三次函数,
是一个三次函数,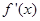 为其导函数.如图所示是函数
为其导函数.如图所示是函数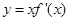 的图像的一部分,则
的图像的一部分,则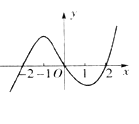
 与
与
 与
与

 ,其图象在
,其图象在 处的切线方程为
处的切线方程为 .
. 的解析式;
的解析式; 的图象与
的图象与 的图象有三个不同的交点,求实数
的图象有三个不同的交点,求实数 的取值范围;
的取值范围;
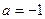 时,求函数的单调区间。
时,求函数的单调区间。 时,讨论函数的单调增区间。
时,讨论函数的单调增区间。 ,使
,使 ,函数有最小值-3?
,函数有最小值-3? 是函数
是函数 的一个极值点,其中
的一个极值点,其中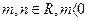
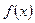 的单调区间
的单调区间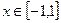 时函数
时函数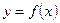 的图象上一任意点的切线斜率恒大于3m,求m的取值范围
的图象上一任意点的切线斜率恒大于3m,求m的取值范围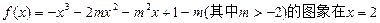 处的切线与直线
处的切线与直线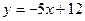 平行.
平行. 的值;
的值; 在区间[0,1]的最小值;
在区间[0,1]的最小值; ,根据上述(I)
,根据上述(I) 、(II)的结论,证明:
、(II)的结论,证明: