题目内容
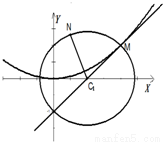
如图,圆C1:(x﹣a)2+y2=r2(r>0)与抛物线C2:x2=2py(p>0)的一个交点
M(2,1),且抛物线在点M处的切线过圆心C1.
(Ⅰ)求C1和C2的标准方程;
(Ⅱ)若点N为圆C1上的一动点,求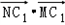 的取值范围.
的取值范围.
M(2,1),且抛物线在点M处的切线过圆心C1.
(Ⅰ)求C1和C2的标准方程;
(Ⅱ)若点N为圆C1上的一动点,求
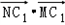 的取值范围.
的取值范围.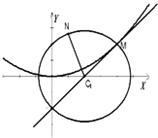
解:(Ⅰ)由题意可得:把M(2,1)代入C2:x2=2py(p>0),解得p=2,
所以C2:x2=4y
由 得
得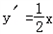 ,
,
所以C2在点M处的切线方程为y﹣1=x﹣2,
令y=0有x=1.
因为抛物线在点M处的切线过圆心C1,所以圆心C1(1,0),
又因为M (2,1)在圆C1上所以(2﹣1)2+1=r2,
解得r2=2,
故C1:(x﹣1)2+y2=2
(Ⅱ)设N(x,y),则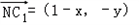 ,
, ,
,
所以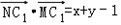 ,
,
令x+y﹣1=t,代入(x﹣1)2+y2=2得(y﹣t)2+y2=2,
整理得2y2﹣2ty+t2﹣2=0
由△=4t2﹣8(t2﹣2)≥0得﹣2≤t≤2
所以 的取值范围为[﹣2,2].
的取值范围为[﹣2,2].
所以C2:x2=4y
由
 得
得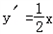 ,
,所以C2在点M处的切线方程为y﹣1=x﹣2,
令y=0有x=1.
因为抛物线在点M处的切线过圆心C1,所以圆心C1(1,0),
又因为M (2,1)在圆C1上所以(2﹣1)2+1=r2,
解得r2=2,
故C1:(x﹣1)2+y2=2
(Ⅱ)设N(x,y),则
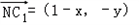 ,
, ,
,所以
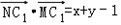 ,
,令x+y﹣1=t,代入(x﹣1)2+y2=2得(y﹣t)2+y2=2,
整理得2y2﹣2ty+t2﹣2=0
由△=4t2﹣8(t2﹣2)≥0得﹣2≤t≤2
所以
 的取值范围为[﹣2,2].
的取值范围为[﹣2,2].

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
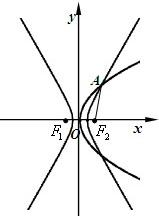 如图,抛物线C1:y2=8x与双曲线
如图,抛物线C1:y2=8x与双曲线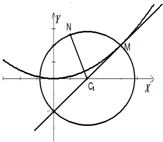 如图,圆C1:(x-a)2+y2=r2(r>0)与抛物线C2:x2=2py(p>0)的一个交点M(2,1),且抛物线在点M处的切线过圆心C1.
如图,圆C1:(x-a)2+y2=r2(r>0)与抛物线C2:x2=2py(p>0)的一个交点M(2,1),且抛物线在点M处的切线过圆心C1.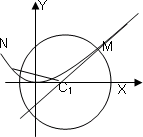
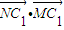 的取值范围.
的取值范围.