题目内容
已知实数x，y满足
，则（x-1）2+y2的最大值为（ ）
|
A、
| ||
| B、2 | ||
| C、4 | ||
| D、5 |
分析：作出可行域，给目标函数赋予几何意义：到（1，0）距离的平方，据图分析可得到点A与（1，0）距离最大．
解答：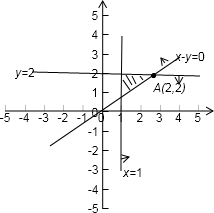
解：作出可行域
（x-1）2+y2表示点（x，y）与（1，0）距离的平方，
由图知，可行域中的点A与（1，0）最远
故（x-1）2+y2最大值为（2-1）2+22=5
故选项为D
解：作出可行域（x-1）2+y2表示点（x，y）与（1，0）距离的平方，
由图知，可行域中的点A与（1，0）最远
故（x-1）2+y2最大值为（2-1）2+22=5
故选项为D
点评：本题考查画不等式组表示的可行域，利用可行域求目标函数的最值．
练习册系列答案
相关题目
已知实数x，y满足
-
=1(a＞0，b＞0)，则下列不等式中恒成立的是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、|y|＜
| ||
B、y＞-
| ||
C、|y|＞-
| ||
D、y＜
|