题目内容
(2012•海淀区一模)对于集合M,定义函数fM(x)=
对于两个集合M,N,定义集合M△N={x|fM(x)•fN(x)=-1}.已知A={2,4,6,8,10},B={1,2,4,8,16}.
(Ⅰ)写出fA(1)和fB(1)的值,并用列举法写出集合A△B;
(Ⅱ)用Card(M)表示有限集合M所含元素的个数,求Card(X△A)+Card(X△B)的最小值;
(Ⅲ)有多少个集合对(P,Q),满足P,Q⊆A∪B,且(P△A)△(Q△B)=A△B?
|
(Ⅰ)写出fA(1)和fB(1)的值,并用列举法写出集合A△B;
(Ⅱ)用Card(M)表示有限集合M所含元素的个数,求Card(X△A)+Card(X△B)的最小值;
(Ⅲ)有多少个集合对(P,Q),满足P,Q⊆A∪B,且(P△A)△(Q△B)=A△B?
分析:(Ⅰ)根据定义直接得答案;
(Ⅱ)对于已知集合E、F,①若a∈E且a∉F,则Card(E△(F∪{a})=Card(E△F)-1;
②若a∉E且a∉F,则Card(E△(F∪{a})=Card(E△F)+1,据此结论找出满足条件的集合,从而求出Card(X△A)+Card(X△B)的最小值.
(Ⅲ)由P,Q⊆A∪B,且(P△A)△(Q△B)=A△B求出集合P,Q所满足的条件,进而确定集合对(P,Q)的个数.
(Ⅱ)对于已知集合E、F,①若a∈E且a∉F,则Card(E△(F∪{a})=Card(E△F)-1;
②若a∉E且a∉F,则Card(E△(F∪{a})=Card(E△F)+1,据此结论找出满足条件的集合,从而求出Card(X△A)+Card(X△B)的最小值.
(Ⅲ)由P,Q⊆A∪B,且(P△A)△(Q△B)=A△B求出集合P,Q所满足的条件,进而确定集合对(P,Q)的个数.
解答:解:(Ⅰ)结合所给定义知,fA(1)=1,fB(1)=-1,A△B={1,6,10,16}.
(Ⅱ)根据题意可知:对于集合C,X,
①若a∈C且a∉X,则Card(C△(X∪{a})=Card(C△X)-1;
②若a∉C且a∉X,则Card(C△(X∪{a})=Card(C△X)+1.
所以 要使Card(X△A)+Card(X△B)的值最小,2,4,8一定属于集合X;
1,6,10,16是否属于X不影响Card(X△A)+Card(X△B)的值,但集合X不能含有A∪B之外的元素.
所以 当X为集合{1,6,10,16}的子集与集合{2,4,8}的并集时,Card(X△A)+Card(X△B)取到最小值4.
所以Card(X△A)+Card(X△B)的最小值
(Ⅲ)因为 A△B={x|fA(x)•fB(x)=-1},
所以 A△B=B△A.
由定义可知:fA△B(x)=fA(x)•fB(x).
所以 对任意元素x,f(A△B)△C(x)=fA△B(x)•fC(x)=fA(x)•fB(x)•fC(x),
fA△(B△C)(x)=fA(x)•fB△C(x)=fA(x)•fB(x)•fC(x).
所以 f(A△B)△C(x)=fA△(B△C)(x).
所以 (A△B)△C=A△(B△C).
由 (P△A)△(Q△B)=A△B知:(P△Q)△(A△B)=A△B.
所以 (P△Q)△(A△B)△(A△B)=(A△B)△(A△B).
所以 P△Q△∅=∅.
所以 P△Q=∅,即P=Q.
因为 P,Q⊆A∪B,
所以 满足题意的集合对(P,Q)的个数为27=128.
(Ⅱ)根据题意可知:对于集合C,X,
①若a∈C且a∉X,则Card(C△(X∪{a})=Card(C△X)-1;
②若a∉C且a∉X,则Card(C△(X∪{a})=Card(C△X)+1.
所以 要使Card(X△A)+Card(X△B)的值最小,2,4,8一定属于集合X;
1,6,10,16是否属于X不影响Card(X△A)+Card(X△B)的值,但集合X不能含有A∪B之外的元素.
所以 当X为集合{1,6,10,16}的子集与集合{2,4,8}的并集时,Card(X△A)+Card(X△B)取到最小值4.
所以Card(X△A)+Card(X△B)的最小值
(Ⅲ)因为 A△B={x|fA(x)•fB(x)=-1},
所以 A△B=B△A.
由定义可知:fA△B(x)=fA(x)•fB(x).
所以 对任意元素x,f(A△B)△C(x)=fA△B(x)•fC(x)=fA(x)•fB(x)•fC(x),
fA△(B△C)(x)=fA(x)•fB△C(x)=fA(x)•fB(x)•fC(x).
所以 f(A△B)△C(x)=fA△(B△C)(x).
所以 (A△B)△C=A△(B△C).
由 (P△A)△(Q△B)=A△B知:(P△Q)△(A△B)=A△B.
所以 (P△Q)△(A△B)△(A△B)=(A△B)△(A△B).
所以 P△Q△∅=∅.
所以 P△Q=∅,即P=Q.
因为 P,Q⊆A∪B,
所以 满足题意的集合对(P,Q)的个数为27=128.
点评:该题是一道与集合相关的信息题,难度较大,高考中很少出现.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
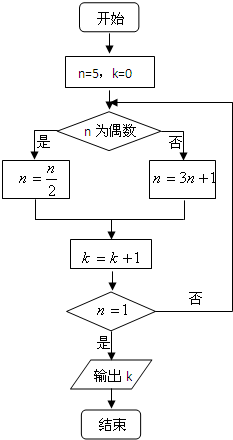 (2012•海淀区一模)执行如图所示的程序框图,输出的k值是( )
(2012•海淀区一模)执行如图所示的程序框图,输出的k值是( )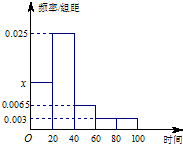 (2012•海淀区一模)某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].
(2012•海淀区一模)某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].